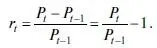Иван Дарушин - Финансовый инжиниринг - инструменты и технологии. Монография

Агрегирующим показателем, учитывающим все эти факторы, является волатильность цены , которая включает в себя величину, скорость и частоту изменений. Само слово волатильность ( volatility ) означает изменчивость, следовательно, возникает вопрос, как оценить волатильность и можно ли ее использовать в качестве показателя ценового риска. Что касается последнего, то сразу скажем, что именно волатильность является наилучшим показателем ценового риска, поскольку возможность отклонения будущих значений цен от ожидаемых будет тем больше, чем больше, чаще и быстрее изменяются цены, т. е. чем выше волатильность. Что же касается вопроса об измерении волатильности, то отметим, что на сегодняшний день не существует общепринятого показателя волатильности. Возможно, это связано с тем, что показатель является агрегированным, учитывающим несколько факторов изменчивости. В любом случае нам необходимо предложить хотя бы и не столь универсальный, но подходящий по целям анализа схожий показатель.

Таким показателем является стандартное отклонение цен или доходностей финансового инструмента. Сразу же отметим, что само по себе стандартное отклонение цены (доходности) не является полным аналогом введенного понятия волатильности, т. к. показатель характеризует лишь относительную величину изменений, не принимая во внимание частоты и скорости измерений, более того, способ расчета показателя не является безукоризненным и лишенным недостатков, о чем речь пойдет ниже. Однако финансисты обычно отождествляют волатильность и стандартное отклонение 101. Более того, некоторые финансовые учреждения используют термин единица волатильности (изменчивости) для обозначения единицы стандартного отклонения.

В теории волатильности выделяют несколько ее видов. Волатильность, определенную по историческим данным о движении стоимости ценной бумаги, называют статистической (исторической) волатильностью ( statistical volatility ) 102. Кроме того, существуют подходы, в которых значение волатильности «восстанавливается» из стоимостей обращающихся опционов, ценообразование которых, в соответствии с формулой Блэка–Шоулза, предполагает использование данного параметра. При оценке теоретической стоимости опциона, в соответствии с этой моделью, используются данные о статистической волатильности. Зная рыночную стоимость опциона, инвестор может использовать ее значение для того, чтобы определить значение волатильности, используемой в формуле как один из переменных параметров. Полученное в результате значение называют подразумеваемой или вмененной волатильностью ( implied volatility ) 103. Оба указанных вида волатильности применяются в перспективном анализе, когда инвестор определяет значение риска в будущем в момент принятия инвестиционного решения. Если же расчеты проводятся постфактум, в процессе анализа рынка и его изменений, волатильность называют реализованной или актуальной ( realized or actual volatility ).

Традиционная методика расчета волатильности основана на использовании показателя стандартного отклонения. Для ее использования инвестору должны быть известны значения цены актива на t моментов в прошлом, другими словами, он имеет ряд периодических наблюдений за ценой актива. Отметим, что в качестве выбранных цен могут использоваться разные значения цены, это могут быть цены закрытия, открытия, средние цены рынка, цены спроса или предложения. Выбор конкретной цены зависит от целей анализа и дальнейших действий инвестора.

Так как цены различных инструментов рынка могут быть несопоставимы, а расчет риска осуществляется в том числе и для сравнения инструментов, то необходимо рассчитывать риск на основании относительных показателей. Поэтому ряд цен инструмента обычно трансформируется в ряд доходностей. При расчете доходностей необходимо принимать во внимание периодичность наблюдений за ценой актива. Так, если между моментами наблюдений были разные промежутки времени, необходимо перевести все показатели доходности к одной длительности, напр., в проценты годовых.

Что касается вида используемой в расчетах доходности, то здесь существуют различные подходы. Отечественные авторы обычно рекомендуют использовать простую процентную доходность (2.4) 104.

(2.4)

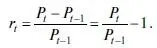
В западных источниках традиционно используют логарифмическую доходность, предполагающую непрерывное начисление процентов (2.5) 105. Отметим, что с выбором формулы для расчета доходности тесно связано предположение о форме распределения доходности ценной бумаги. Так, если предполагается нормальное распределение, то используется простая доходность. Логнормальное распределение предполагает использование логарифмической доходности.