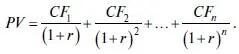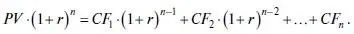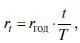Иван Дарушин - Финансовый инжиниринг - инструменты и технологии. Монография

Использование сложных процентов предполагает реинвестирование промежуточных денежных потоков под ставку дисконтирования.

Убедимся в этом путем следующих рассуждений. Рассчитаем приведенную стоимость (PV) денежного потока (CF1, CF2, … , CFn), исходя из ставки дисконтирования r (формула 2.1).

(2.1)

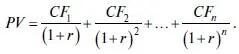
Домножим обе части равенства (2.1) на множитель (1 + r) n . Полученное равенство также будет истинным (формула 2.2).

(2.2)

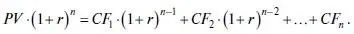
Заметим, что в левой части равенства (2.2.) получена будущая стоимость текущей стоимости инвестиции. Исходя из того, что ставка дисконтирования представляет собой доходность доступной инвестиционной альтернативы аналогичного уровня риска, эта будущая стоимость и в самом деле может быть получена инвестором к концу срока.

Обратимся к сумме в правой части равенства (2.2). Каждое слагаемое в ней представляет собой будущую стоимость соответствующего элемента денежного потока, наращенную к концу срока инвестиции. Действительно, первый элемент денежного потока ( CF 1 ) до конца срока должен быть реинвестирован ( n – 1) раз, последний элемент ( CF n ) – не реинвестируется. А теперь зададимся следующим вопросом. Можно ли утверждать, что в будущем у инвестора сохранится возможность реинвестировать денежные потоки под ставку, равную доходности инвестиционной альтернативы, доступной в настоящий момент времени? По всей видимости, ответ должен быть отрицательным. Это связано с тем, что сроки будущего реинвестирования будут меньше первоначального срока инвестиции, следовательно, для них будет характерен другой уровень риска и другие ставки. Сомнительно также существование выбранной инвестиционной альтернативы и ее доступность на весь период инвестирования.

Очевидно, что реинвестирование в будущем будет осуществляться под другие значения ставок, которые в данный момент неизвестны. Следовательно, рассмотренные равенства (2.1 и 2.2) недостижимы на практике и представляют собой исключительно теоретическую модель оценки текущей и будущей стоимости инвестиции. В любом случае полученная оценка будет носить условный характер, имеющий очень отдаленное отношение к реальной стоимости финансового инструмента.

Отметим, что указанный недостаток модели DCF отсутствует для инструментов, в которых нет промежуточных выплат (дисконтные облигации, краткосрочные инструменты и ряд других). Именно на этом факте основывается ряд современных подходов к оценке стоимости.

Период ставки дисконтирования должен соответствовать периоду анализа. Если в качестве периода анализа выбран один год, то необходимо использовать ставку в процентах годовых. При использовании меньших по длительности периодов анализа необходимо использовать ставки соответствующих периодов. А т. к. традиционно все ставки указываются в процентах годовых, то необходимо переводить их в ставки за соответствующий период. Для этой процедуры обычно используется следующая формула (2.3) 88:

(2.3)

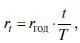
где

r t – ставка за период (должна соответствовать периоду анализа);

r год– ставка в процентах годовых;

t – период анализа;

T – количество дней в году (базис расчета).

Казалось бы, данный расчет не представляет никаких трудностей, однако это не совсем так. Основная проблема заключается в предположении о том, что ставки внутри года изменяются линейно. На первый взгляд может показаться, что это предположение не содержит никакого противоречия, так как при расчетах всегда используется такая техника пересчета ставок. Однако если используются сложные проценты, то реальная (эффективная) ставка, по которой мы получим доход, окажется выше при нескольких начислениях дохода в течение года. Необходимо понимать, что традиционная техника пересчета процентов годовых в проценты за период может быть использована только для расчета номинальных ставок, но в то же время при расчете стоимости инвестиций необходимо учитывать эффективные ставки. Мы получаем противоречие, которое хотя и может быть решено, но зачастую не принимается во внимание, а это снижает качество расчетов и может исказить результат.