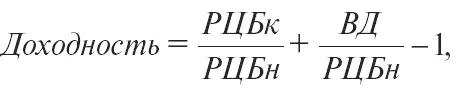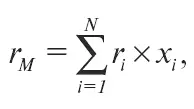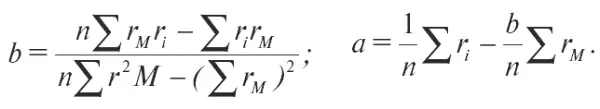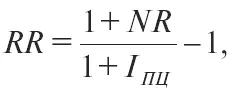Галина Шерстнева - Финансовая статистика - конспект лекций

Доходность ценной бумаги за конкретный период может быть представлена в виде суммы двух величин, одна из которых зависит от изменения рыночной цены (курса) данной ценной бумаги за этот период, а другая – от выплаты доходов по этой бумаге. Следовательно, формула принимает следующий вид:

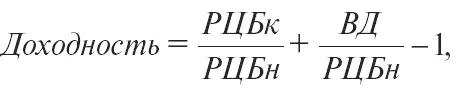
где РЦБн – рыночная цена ценной бумаги в начале периода;

РЦБк – рыночная цена ценной бумаги в конце периода;

ВД – выплаты доходов по ценной бумаге за период.

Соответственно доходность акций по этой формуле рассчитывается следующим образом:

Доходность = (2230/1970 + 570/1970) – 1 = 0,42.

Так как на фондовом рынке продается много различных ценных бумаг, имеющих разную доходность, то средняя рыночная доходность всех циркулирующих на рынке акций (r м) определяется по формуле:

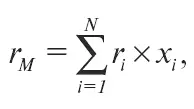
где r i – доходность i-й акции (в долях единицы);

x i – относительная рыночная стоимость i-й акции, равная совокупной рыночной стоимости всех выпущенных акций этого наименования, деленной на сумму совокупных рыночных стоимостей всех присутствующих на рынке акций;

N – количество наименований всех имеющихся на рынке акций.

В основном в качестве r iприменяется отношение рыночной стоимости данной ценной бумаги в конце анализируемого периода к ее рыночной стоимости в начале этого периода, а используемые показатели называются рыночными индексами. В мировой практике применяется ряд таких показателей, несколько отличающихся алгоритмами расчета (например, Standart amp; Poor's Stock Price Index, представляющий собой средневзвешенную величину курсов акций 500 крупнейших корпораций США). В России по подобной методике рассчитывается индекс «РТС-Интерфакс», обобщающий данные об изменении рыночной стоимости 100 обращающихся на российском рынке наиболее ликвидных акций, а также известен индекс AK amp; M и некоторые другие.

Для эффективной работы на фондовом рынке необходимо знать, как доходность конкретного наименования акций (или портфеля акций конкретного инвестора) связана со средней рыночной доходностью всей совокупности акций, т. е. с рыночным индексом. Для этого применяются статистические модели.

Простейшая линейная модель предусматривает существование следующей связи:

где r i – доход по ценной бумаге i за определенный период;

r M – доход, исчисленный по рыночному индексу за определенный период;

a и b – неизвестные параметры (коэффициенты регрессии);

e – величина случайной ошибки, характеризующая отклонение от теоретически предполагаемой связи.

Методом наименьших квадратов решается задача определения a и b . Для чего важно иметь значения r i и r м за n последовательных периодов (например, месяцев). В результате вычислений получаются следующие результаты:

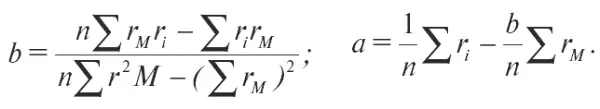
Бета (коэффициент b)– это важный статистический показатель рынка ценных бумаг. Он оценивает изменение доходности определенных акций в соответствии с динамикой рыночного индекса. Если доходность ценных бумаг изменяется так же, как рыночный индекс, то такие ценные бумаги имеют b = 1. Бумаги, по которым b > 1, обладают большей изменчивостью, чем рыночный индекс, и они являются более рискованными, чем рынок в целом. А бумаги, имеющие b < 1, менее рискованны, чем рынок в целом. Допустим, что коэффициент b = 2, тогда при росте среднерыночной доходности на 1 % доходность по данной инвестиции вырастет на 2 %.

В показателях доходности ценных бумаг в условиях инфляции содержится компонента, обусловленная ростом цен, для устранения которой используется индекс потребительских цен:

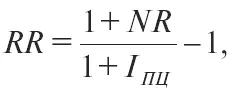
где RR – реальная доходность за год в долях единицы;

NR – номинальная доходность за год в долях единицы;

I пц – индекс потребительских цен за год (в долях единицы).

А для приближенных вычислений используют формулу:

Анализ эффективности намечаемых инвестиций включает в себя принятие решений о приобретении средств производства, которые используются в течение длительного времени. Следовательно, решения об инвестициях влияют на работу фирмы в течение длительного периода, что делает данный анализ особенно важным при определении стратегии компании, он превращается, по сути, в прогнозный анализ.