DNBLF — запаздывание в нормальном портфеле заказов на заводе (недели).
Уравнение 14–25 определяет исходное число не начатых производством заказов на пополнение запаса как произведение установившегося потока заказов, удовлетворяемых из запасов RFIF, и нормальной продолжительности нахождения заказа в портфеле не начатых производством заказов DNBLF (численное значение этой величины приводится после уравнения 14–67).
Аналогичное уравнение может быть записано для задолженности по работам, выполняемым с целью непосредственного удовлетворения требований покупателей:
BLCF.K=BLCFJ+(DT)(RMOF.JK— PCOF.JK),
14–26,
L
BLCF=(RRF — RFIF)(DNBLF),
14–27,
N
где
BLCF — портфель не начатых производством заказов покупателей (единицы);
RMOF — темп поступления требований покупателей на завод (единицы в неделю);
PCOF — производство продукции по заказам покупателей (единицы в неделю);
RRF — темп поступления требований на завод (единицы в неделю);
RFIF — темп требований, удовлетворяемых из запасов завода (единицы в неделю);
DNBLF — запаздывание в нормальном портфеле заказов на заводе (недели).
Теперь необходимо отобразить распределение производственного персонала по каждому из потоков заказов. В нормальных условиях оба портфеля заказов были смешаны, то есть не отдавалось какого-либо приоритета ни одному из рассматриваемых потоков. Это означает, что распределение рабочей силы производилось пропорционально имевшемуся в каждом из потоков числу не начатых производством заказов. Следовательно, именно таким и должен был быть образ деятельности в нормальной ситуации. Однако могут возникнуть такие промежутки времени, в течение которых имеющийся производственный персонал может произвести большее количество продукции по сравнению с числом заказов в портфеле в этот период. В подобных случаях число не начатых производством заказов не должно стать отрицательным, наоборот, часть рабочей силы переключается на производство с целью накопления запасов.
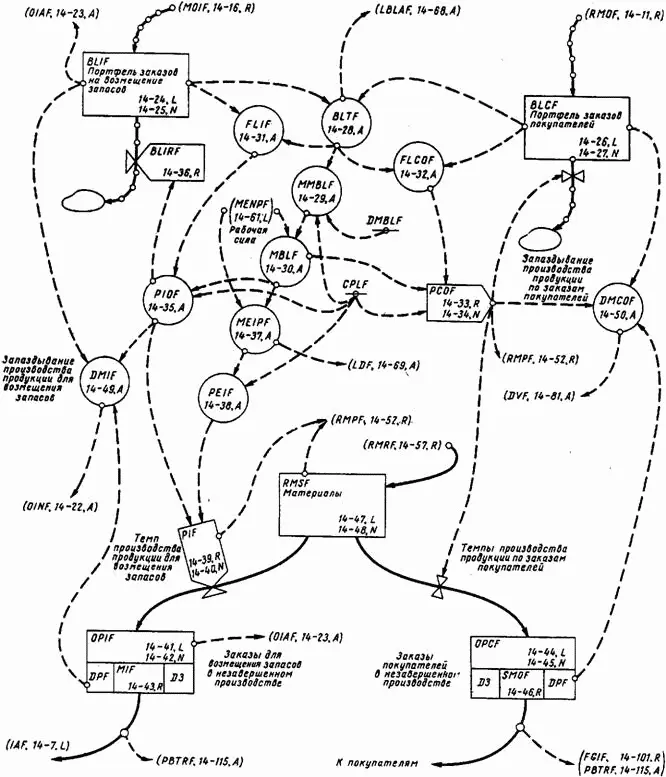
Приводимые ниже уравнения описывают распределение рабочей силы с учетом приведенных соображений.
Первое уравнение определяет суммарный располагаемый портфель заказов:
BLTF.K=BLIF.K+BLCF.K,
14–28,
А
где
BLTF — общий портфель невыполненных заказов на заводе (единицы);
BLIF — портфель заказов на предприятии на возмещение запасов (единицы);
BLCF — портфель заказов покупателей на заводе (единицы).
Задолженность по заказам не должна сокращаться ниже некоторой величины, эквивалентной минимальному времени подготовки заказов к запуску в производство. Это минимальное запаздывание в портфеле невыполненных заказов определяет максимально возможный темп запуска заказов в производство, что в свою очередь определяет максимальную численность рабочих, которые могут быть эффективно использованы при данном запуске. Любое превышение этого количества рабочей силы приведет к изготовлению продукции, превышающей заказанную для пополнения запаса:
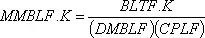 ,
,
14-29,
A
где
MMBLF —максимальная численность рабочих, необходимых для изготовления продукции в соответствии с портфелем заказов на заводе (человек);
BUFF — общий портфель заказов на заводе (единицы);
DMBLF —минимальное запаздывание в портфеле заказов на заводе (недели);
CPLF — константа, производительность труда на заводе (единицы за человеко-неделю).
В приведенном уравнении взято отношение общей задолженности по заказам к минимальному запаздыванию в портфеле не начатых производством заказов, необходимому для подготовки их запуска в производство. Это отношение определяет максимальный темп, с которым заказы могут поступать в производство. Затем этот темп делится на величину производительности труда с тем, чтобы определить максимальную численность рабочих, которые могут быть использованы для изготовления продукции по поступившим заказам.
Минимальное время подготовки заказов к запуску в производство DMBLF в нашем примере составляет одну неделю; производительность труда CPLF, которая не оказывает влияния на динамику системы, мы приняли равной 2 2/ 3единицы в человеко-неделю.
Численность рабочих, привлекаемых к изготовлению продукции в соответствии с портфелем заказов, должна быть либо меньше располагаемой, либо меньше допустимой (как это определено уравнением 14–29):
Читать дальше


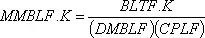 ,
,






![Джей Джей Барридж - Секрет рапторов [litres]](/books/420944/dzhej-dzhej-barridzh-sekret-raptorov-litres-thumb.webp)



