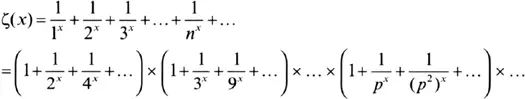G.H. Hardy wrote that he was ‘interested in mathematics only as a creative art’. Even for the French mathematicians in Napoleon’s academies, the buzz of doing mathematics came not from its practical application but from its inner beauty. The aesthetic experiences of doing mathematics or listening to music have much in common. Just as you might listen to a piece of music over and over and find new resonances previously missed, mathematicians often take pleasure in re-reading proofs in which the subtle nuances that make it hang together so effortlessly gradually reveal themselves. Hardy believed that the true test of a good mathematical proof was that ‘the ideas must fit together in a harmonious way. Beauty is the first test: there is no permanent place in the world for ugly mathematics.’ For Hardy, ‘A mathematical proof should resemble a simple and clear-cut constellation, not a scattered Milky Way.’
Both mathematics and music have a technical language of symbols which allow us to articulate the patterns we are creating or discovering. Music is much more than just the minims and crochets which dance across the musical stave. Similarly, mathematical symbols come alive only when the mathematics is played with in the mind.
As Pythagoras discovered, it is not just in the aesthetic realm that mathematics and music overlap. The very physics of music has at its root the basics of mathematics. If you blow across the top of a bottle you hear a note. By blowing harder, and with a little skill, you can start to hear higher notes – the extra harmonics, the overtones. When a musician plays a note on an instrument they are producing an infinity of additional harmonics, just as you do when you blow across the top of the bottle. These additional harmonics help to give each instrument its own distinctive sound. The physical characteristics of each instrument mean that we hear different combinations of harmonics. In addition to the fundamental note, the clarinet plays only those harmonics produced by odd fractions: 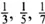 , … The string of a violin, on the other hand, vibrates to create all the harmonics that Pythagoras produced with his urn – those corresponding to the fractions
, … The string of a violin, on the other hand, vibrates to create all the harmonics that Pythagoras produced with his urn – those corresponding to the fractions 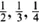 , …
, …
Since the sound of a vibrating violin string is the infinite sum of the fundamental note and all the possible harmonics, mathematicians became intrigued by the mathematical analogue. The infinite sum 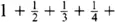 … became known as the harmonic series . This infinite sum is also the answer Euler got when he fed the zeta function with the number x = 1. Although this sum grew only very slowly as he added more terms, mathematicians had known since the fourteenth century that eventually it must spiral off to infinity.
… became known as the harmonic series . This infinite sum is also the answer Euler got when he fed the zeta function with the number x = 1. Although this sum grew only very slowly as he added more terms, mathematicians had known since the fourteenth century that eventually it must spiral off to infinity.
So the zeta function must output the answer infinity when fed the number x = 1. If, however, instead of taking x = 1, Euler fed the zeta function with a number bigger than 1, the answer no longer spiralled off to infinity. For example, taking x = 2 means adding together all the squares in the harmonic series:
This is a smaller number as it does not include all possible fractions found when x = 1. We are now adding only some of the fractions, and Euler knew that this time the smaller sum wouldn’t spiral off to infinity but would home in on some particular number. It had become quite a challenge by Euler’s day to identify a precise value for this infinite sum when x = 2. The best estimate was somewhere around . In 1735, Euler wrote that ‘So much work has been done on the series that it seems hardly likely that anything new about them may still turn up … I, too, in spite of repeated effort, could achieve nothing more than approximate values for their sums.’
Nevertheless, Euler, emboldened by his previous discoveries, began to play around with this infinite sum. Twisting it this way and that like the sides of a Rubik’s cube, he suddenly found the series transformed. Like the colours on the cube, these numbers slowly came together to form a completely different pattern from the one he had started with. As he went on to describe, ‘Now, however, quite unexpectedly, I have found an elegant formula depending upon the quadrature of the circle’ – in modern parlance, a formula depending on the number π = 3.1415 …
By some pretty reckless analysis, Euler had discovered that this infinite sum was homing in on the square of π divided by 6:
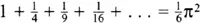
The decimal expansion of , like that of π, is completely chaotic and unpredictable. To this day, Euler’s discovery of this order lurking in the number 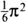 ranks as one of the most intriguing calculations in all of mathematics, and it took the scientific community of Euler’s time by storm. No one had predicted a link between the innocent sum and the chaotic number π.
ranks as one of the most intriguing calculations in all of mathematics, and it took the scientific community of Euler’s time by storm. No one had predicted a link between the innocent sum and the chaotic number π.
This success inspired Euler to investigate the power of the zeta function further. He knew that if he fed the zeta function with any number bigger than 1, the result would be some finite number. After a few years of solitary study he managed to identify the output of the zeta function for every even number. But there was something rather unsatisfactory about the zeta function. Whenever Euler fed the formula for the zeta function with any number less than 1, it would always output infinity. For example, for x = −1 it yields the infinite sum 1 + 2 + 3 + 4 + … The function behaved well only for numbers bigger than 1.
Euler’s discovery of his expression for in terms of simple fractions was the first sign that the zeta function might reveal unexpected links between seemingly disparate parts of the mathematical canon. The second strange connection that Euler discovered was with an even more unpredictable sequence of numbers.
Rewriting the Greek story of the primes
Prime numbers suddenly enter Euler’s story as he tried to put his rickety analysis of the expression for on a sound mathematical footing. As he played with the infinite sums he recalled the Greek discovery that every number can be built from multiplying prime numbers together, and realised that there was an alternative way to write the zeta function. He spotted that every term in the harmonic series, for example 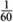 , could be dissected using the knowledge that every number is built from its prime building blocks. So he wrote
, could be dissected using the knowledge that every number is built from its prime building blocks. So he wrote
Instead of writing the harmonic series as an infinite addition of all the fractions, Euler could take just fractions built from single primes, like , and multiply them together. His expression, known today as Euler’s product , connected the worlds of addition and multiplication. The zeta function appeared on one side of the new equation and the primes on the other. In one equation was encapsulated the fact that every number can be built by multiplying together prime numbers:
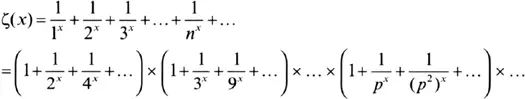
At first sight Euler’s product doesn’t look as if it will help us in our quest to understand prime numbers. After all, it’s just another way of expressing something the Greeks knew more than two thousand years ago. Indeed, Euler himself would not grasp the full significance of his rewriting of this property of the primes.
Читать дальше

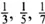 , … The string of a violin, on the other hand, vibrates to create all the harmonics that Pythagoras produced with his urn – those corresponding to the fractions
, … The string of a violin, on the other hand, vibrates to create all the harmonics that Pythagoras produced with his urn – those corresponding to the fractions 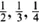 , …
, …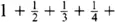 … became known as the harmonic series . This infinite sum is also the answer Euler got when he fed the zeta function with the number x = 1. Although this sum grew only very slowly as he added more terms, mathematicians had known since the fourteenth century that eventually it must spiral off to infinity.
… became known as the harmonic series . This infinite sum is also the answer Euler got when he fed the zeta function with the number x = 1. Although this sum grew only very slowly as he added more terms, mathematicians had known since the fourteenth century that eventually it must spiral off to infinity.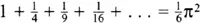
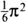 ranks as one of the most intriguing calculations in all of mathematics, and it took the scientific community of Euler’s time by storm. No one had predicted a link between the innocent sum and the chaotic number π.
ranks as one of the most intriguing calculations in all of mathematics, and it took the scientific community of Euler’s time by storm. No one had predicted a link between the innocent sum and the chaotic number π.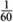 , could be dissected using the knowledge that every number is built from its prime building blocks. So he wrote
, could be dissected using the knowledge that every number is built from its prime building blocks. So he wrote