Marcus Sautoy - The Music of the Primes - Why an unsolved problem in mathematics matters

Irrational numbers and negative numbers allow us to solve many different equations. Fermat’s equation x 3+ y 3= z 3has interesting solutions if you don’t insist, as Fermat had, that x, y and z should be whole numbers. For example, we can choose x = 1 and y = 1, and put z equal to the cube root of 2 – and the equation is solved. But there were still other equations which couldn’t be solved in terms of any of the numbers on the number line.

There seemed to be no number which was a solution to the equation x 2= −1. After all, if you square a number, positive or negative, the answer is always positive. So any number that satisfies this equation is not going to be an ordinary number. But if the Greeks could imagine a number like the square root of 2, without being able to write it down as a fraction, mathematicians began to see that they could make a similar imaginative leap and create a new number to solve the equation x 2= −1. Such a creative jump marks one of the conceptual challenges for anyone learning mathematics. This new number, the square root of minus one, was called an imaginary number and given the symbol i. In contrast, mathematicians began to refer to the numbers that could be found on the number line as real numbers .

To create an answer to this equation, seemingly out of thin air, seems like cheating. Why not accept that the equation has no solution? That is one way forward, but mathematicians like to be more optimistic. Once we accept the idea that there is a new number that does solve this equation, the advantages of this creative step far outweigh any initial unease. Once named, its existence seems inevitable. It no longer feels like an artificially created number but a number that had been there all along, unobserved until we’d asked the right question. Eighteenth-century mathematicians had been loath to admit there could be any such numbers. Nineteenth-century mathematicians were brave enough to believe in new modes of thought which challenged the accepted ideas of what constituted the mathematical canon.

Frankly, the square root of −1 is as abstract a concept as the square root of 2. Both are defined as solutions to equations. But would mathematicians have to start creating new numbers for every new equation that came along? What if we want solutions to an equation like x 4= −1? Are we going to have to use more and more letters in our attempts to name all these new solutions? It was with some relief that Gauss finally proved, in his doctoral thesis of 1799, that no new numbers were needed. Using this new number i, mathematicians could finally solve any equation they might come across. Every equation had a solution that consisted of some combination of ordinary real numbers (the fractions and irrational numbers) and this new number, i.

The key to Gauss’s proof was to extend the picture we already had of ordinary numbers as lying on a number line: a line running east-west on which each point represents a number. These were the real numbers familiar to mathematicians since the Greeks. But there was no room on the line for this new imaginary number, the square root of −1. So Gauss wondered what would happen if you created a new direction. What if one unit north of the number line were used to represent i? All the new numbers that were needed to solve equations were combinations of i and ordinary numbers, for example 1 + 2i. Gauss realised that on this two-dimensional map there was a point corresponding to every possible number. The imaginary numbers then simply became coordinates on a map. The number 1 + 2i was represented by the point reached by travelling one unit east and two units north.

Gauss would interpret these numbers as sets of directions in his map of the imaginary world. To add two imaginary numbers A + B i and C + D i just meant following two sets of directions, one after the other. For example, adding together 6 + 3i and 1 + 2i gets you to the location 7 + 5i.

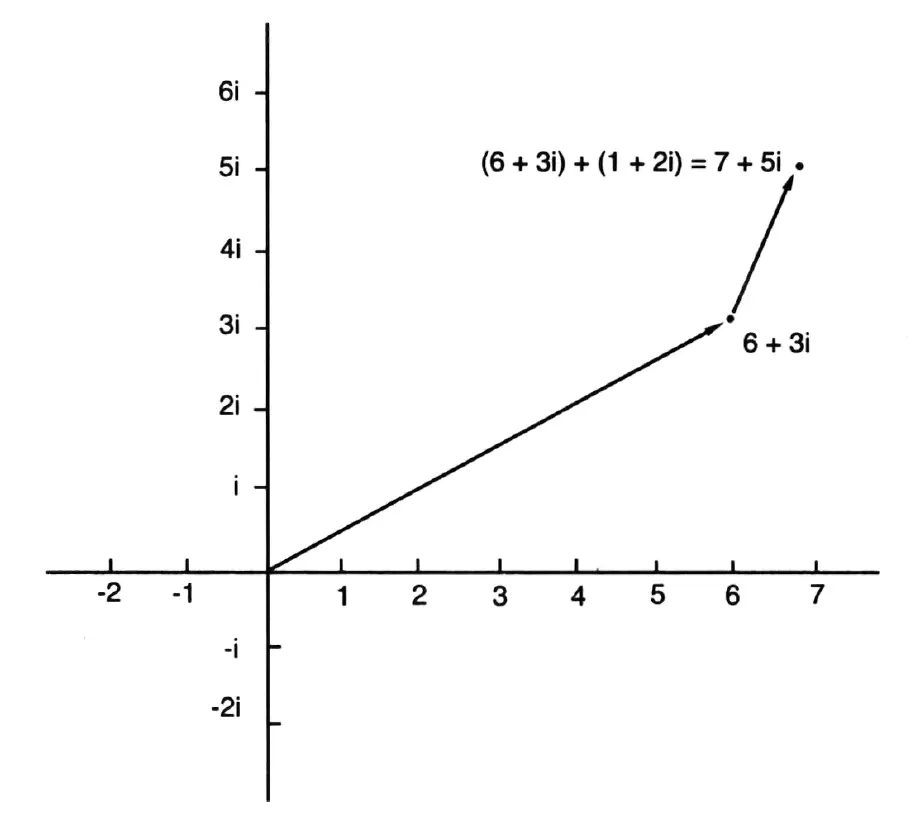
Following directions – how to add two imaginary numbers.

Although this was a very potent picture. Gauss was to keep his map of the imaginary world hidden from public view. Once he had built his proof, he removed the graphic scaffolding so that no trace of his vision remained. He was aware that pictures in mathematics were regarded with some suspicion during this period. The dominance of the French mathematical tradition during Gauss’s youth meant that the preferred pathway to the mathematical world was the language of formulas and equations, a language that went hand in hand with the utilitarian approach to the subject. There were also other reasons for this aversion to images.

For several hundred years, mathematicians had believed that pictures had the power to mislead. After all, the language of mathematics had been introduced to tame the physical world. In the seventeenth century, Descartes had attempted to turn the study of geometry into pure statements about numbers and equations. ‘Sense perceptions are sense deceptions’ was his motto. Riemann had come to dislike this denial of the physical picture when he’d been reading Descartes in the comfort of Schmalfuss’s library.

Mathematicians around the turn of the nineteenth century had been burnt by an erroneous pictorial proof of a formula describing the relationship between the number of corners, edges and faces of geometric solids. Euler had conjectured that if a solid has C corners, E edges and F faces, then the numbers C, E and F must satisfy the relationship C − E + F = 2. For example, a cube has 8 corners, 12 edges and 6 faces. The young Cauchy had himself constructed a ‘proof’ in 1811 based on pictorial intuition, but was rather shocked to be shown a solid which didn’t satisfy this formula – a cube with a hole at its centre.

The ‘proof’ had missed the possibility that a solid might contain such a hole. It was necessary to introduce an extra ingredient into the formula which kept track of the number of holes in the solid. Having been tricked by the power of pictures to hide perspectives that weren’t initially apparent, Cauchy sought refuge in the security that formulas seemed to provide. One of the revolutions he effected was to create a new mathematical language which allowed mathematicians to discuss the concept of symmetry in a rigorous way without the need for pictures.

Gauss knew that his secret map of imaginary numbers would be anathema to mathematicians at the end of the eighteenth century, so he omitted it from his proof. Numbers were things you added and multiplied, not drew pictures of. Gauss eventually came clean some forty years later about the scaffolding he had used in his doctorate.

Even without Gauss’s map, Cauchy and other mathematicians had begun to explore what happens if you extend the idea of functions to this new world of imaginary numbers rather than sticking to real numbers. To their surprise, these imaginary numbers opened up new connections between seemingly unrelated parts of the mathematical world.

A function is like a computer program in which you input one number, a calculation is made, and another number is output. The function might be defined by some simple equation like x 2+ 1. When you input a number, for example 2, the function calculates 2 2+ 1 and outputs 5. Other functions are more complicated. Gauss was interested in the function that counted the number of primes. You input a number x , and the function tells you how many primes there are up to x . Gauss had denoted this function by π( x ). The graph of this function is a climbing staircase, as shown on p. 50. Every time the input encounters a prime number, the output jumps another step. As x goes from 4.9 to 5.1, the number of primes increases from two to three to register the new prime, 5.