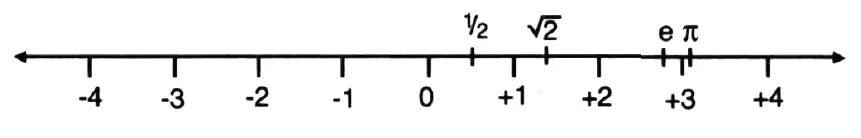Marcus Sautoy - The Music of the Primes - Why an unsolved problem in mathematics matters

Riemann made friends with several young researchers in Dirichlet’s seminars who were equally fired up by their passion for mathematics.

Other forces were also bubbling away in Berlin. The revolution of 1848 that swept away the French monarchy spread from the streets of Paris throughout much of Europe. It found its way to the streets of Berlin while Riemann was studying there. According to accounts of his contemporaries, it had a profound impact on him. On one of the few occasions in his life on which he joined with those around him on anything other than an intellectual level, he enlisted in the student corps defending the king in his Berlin palace. It is reputed that he did a continuous sixteen-hour stint on the barricades.

Riemann’s response to the mathematical revolution spreading from the Paris academies was not that of a reactionary. Berlin was importing not only political propaganda from Paris, but also many of the prestigious journals and publications coming out of the academies. Riemann received the latest volumes of the influential French journal Comptes Rendus and holed himself up in his room to pore over papers by the mathematical revolutionary Augustin-Louis Cauchy.

Cauchy was a child of the Revolution, born a few weeks after the fall of the Bastille in 1789. Undernourished by the little food available during those years, the feeble young Cauchy preferred to exercise his mind rather than his body. In time-honoured fashion, the mathematical world provided a refuge for him. A mathematical friend of Cauchy’s father, Lagrange, recognised the young boy’s precocious talent and commented to a contemporary, ‘You see that little young man? Well! He will supplant all of us in so far as we are mathematicians.’ But he had interesting advice for Cauchy’s father. ‘Don’t let him touch a mathematical book till he is seventeen.’ Instead, he suggested stimulating the boy’s literary skills so that when eventually he returned to mathematics he would be able to write with his own mathematical voice and not one he had picked up from the books of the day.

It proved to be sound advice. Cauchy developed a new voice that was irrepressible once the floodgates protecting Cauchy from the outside world had been reopened. Cauchy’s output grew to be so immense that the journal Comptes Rendus had to impose a page limit on articles it printed that is strictly adhered to even today. Cauchy’s new mathematical language was too much for some of his contemporaries. The Norwegian mathematician Niels Henrik Abel wrote in 1826, ‘Cauchy is mad … what he does is excellent but very muddled. At first I understood practically none of it; now I see some of it more clearly.’ Abel goes on to observe that of all the mathematicians in Paris, Cauchy was the only one doing ‘pure mathematics’ whilst others ‘busy themselves exclusively with magnetism and other physical subjects … he is the only one who knows how mathematics should be done’.

Cauchy was to land himself in trouble with the authorities in Paris for steering students away from practical applications of mathematics. The director of the École Polytechnique, where Cauchy was lecturing, wrote to him criticising him for his obsession with abstract mathematics: ‘It is the opinion of many persons that instruction in pure mathematics is being carried too far at the École and that such an uncalled for extravagance is prejudicial to the other branches.’ So it was perhaps no wonder that Cauchy’s work would be appreciated by the young Riemann.

So exciting were these new ideas that Riemann almost became a recluse. His contemporaries were to see nothing of him while he waded through Cauchy’s output. Several weeks later Riemann resurfaced, declaring that ‘this is a new mathematics’. What had captured Cauchy and Riemann’s imagination was the emerging power of imaginary numbers.

The square root of minus one, the building block of imaginary numbers, seems to be a contradiction in terms. Some say that admitting the possibility of such a number is what separates the mathematicians from the rest. A creative leap is required to gain access to this bit of the mathematical world. At first sight it looks as if it has nothing to do with the physical world. The physical world seems to be built on numbers whose square is always a positive number. Imaginary numbers, however, are more than just an abstract game. They hold the key to the twentieth-century world of subatomic particles. On a larger scale, aeroplanes would not have taken to the skies without engineers taking a journey through the world of imaginary numbers. This new world provides a flexibility denied to those who stick to ordinary numbers.

The story of how these new numbers were discovered begins with the need to solve simple equations. As the ancient Babylonians and Egyptians recognised, if seven fish were to be divided between three people, for example, fractional numbers – , and so on – would have to come into the equation. By the sixth century BC, the Greeks had discovered while exploring the geometry of triangles that these fractions were sometimes incapable of expressing the lengths of the sides of a triangle. Pythagoras’ theorem forced them to invent new numbers that couldn’t be written as simple fractions. For example, Pythagoras could take a right-angled triangle whose two shortest sides are one unit long. His famous theorem then told him that the longest side had length x , where x is a solution of the equation x 2= 1 2+ 1 2= 2. In other words, the length is the square root of 2.

Fractions are the numbers whose decimal expansions have a repeating pattern. For example, In contrast, the Greeks could prove that the square root of 2 is not equal to a fraction. However far you calculate the decimal expansion of the square root of 2, it will never settle down into such a repeating pattern. The square root of 2 starts off 1.414213562 … Riemann used to idle away the hours calculating more and more of these decimal places during his years in Göttingen. His record was thirty-eight places, no mean feat without a computer but perhaps more a reflection on the dull Göttingen nightlife and Riemann’s shy persona that this was his evening entertainment. Nonetheless, however far Riemann calculated, he knew that he could never write down the complete number or discover a repeating pattern.

To capture the impossibility of expressing such numbers in any way other than as solutions to equations such as x 2= 2, mathematicians called them irrational numbers . The name reflected mathematicians’ sense of unease at their inability to write down precisely what these numbers were. Nevertheless, there was still a sense of the reality of these numbers since they could be seen as points marked on a ruler, or on what mathematicians call the number line. The square root of 2, for example, is a point somewhere between 1.4 and 1.5. If one could make a perfect Pythagorean right-angled triangle with the two short sides one unit long, then the location of this irrational number could be determined by laying the long side against the ruler and marking off the length.

The negative numbers were discovered similarly out of attempts to solve simple equations such as x + 3 = 1. Hindu mathematicians proposed these new numbers in the seventh century AD. Negative numbers were created in response to the growing world of finance, as they were useful for describing debt. It took European mathematicians another millennium before they were happy to admit the existence of such ‘fictitious numbers’, as they were called. Negative numbers took their place on the number line stretching out to the left of zero.

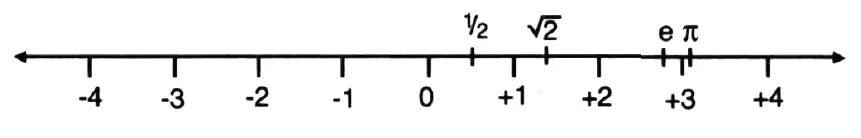
The real numbers – every fraction, negative number or irrational number is represented by a point on the number line.