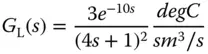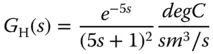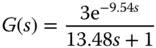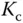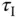With sampling interval (s), the closed-loop step responses are compared in Figure 1.19, where the IP controller structure is used to reduce overshoot to the step reference signal. It is clearly seen that the closed-loop system with is stable; however, with it is not.
Now, we evaluate the closed-loop performance for a PID controller with filter, where the filter time constant is chosen to be . Based on Table 1.5, the PID controller parameters are calculated as for , , , , and for , , , .
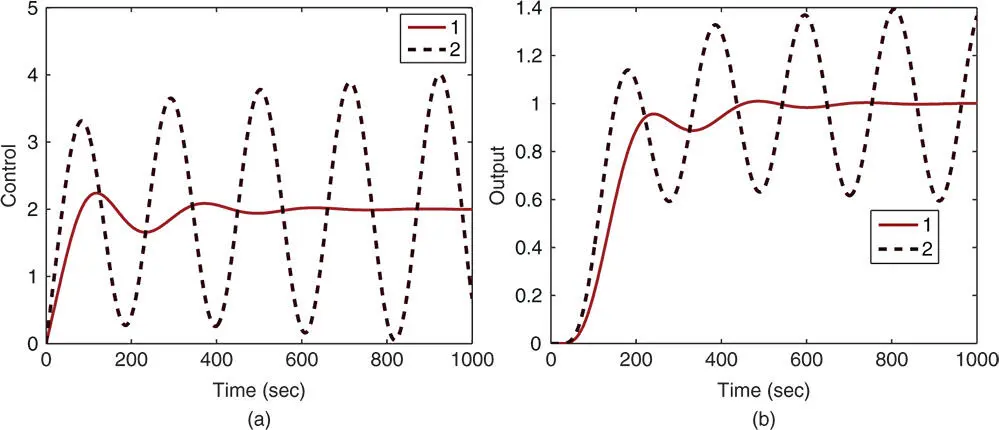
Figure 1.19Comparison of closed-loop responses using Padula and Visioli PI controller ( Example 1.8). (a) Control signal. (b) Output. Key: line (1) tuning rule with 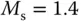 ; line (2) tuning rule with
; line (2) tuning rule with 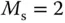 .
.

Figure 1.20Comparison of closed-loop responses using Padula and Visioli PID controller ( Example 1.8). (a) Control signal. (b) Output. Key: line (1) tuning rule with 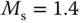 ; line (2) tuning rule with
; line (2) tuning rule with 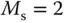 .
.
With the same sampling interval , and both proportional and derivative control on output only (IPD structure) where the derivative filter time constant is selected as , the closed-loop responses are simulated. Figure 1.20 compares the closed-loop responses. Both tuning rules lead to stable closed-loop control systems. It is seen that there are overshoots in both reference responses, which was caused by the quite large derivative gains.
1.5.2 Fired Heater Control Example
A fired heater using gas fuel is a heating furnace that is typically used for household heating in the winter times. In this case study, the input to the heating furnace is the feed rate of the gas fuel and the output is the heater outlet or the room temperature in a house. Because the temperature sensors are located away from the heating source, there is a time delay in the measured temperature when the input feed rate changes. Additionally, depending on the operating conditions of the input feed rate, the dynamic response of the temperature is different. Two transfer function models are given in Ralhan and Badgwell (2000) to describe the operations of a gas fired heater at a low fuel operation and a high fuel operation. At the low fuel operating condition, the transfer function is described as
(1.58) 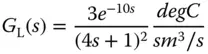
and at the high fuel operating condition,
(1.59) 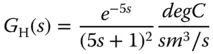
where the time constant is in minutes. Note that there are dramatically differences in time delay and the steady-state gain of the transfer function models.
In this study, we will introduce the effect of input disturbance in the closed-loop simulation by adding a step signal with negative magnitude to the control signal. This input disturbance represents a sudden change in the process that causes the output temperature drop. The effect of this disturbance is further discussed in Chapter 2.
In this example, we will show how to use the tuning rules to find the PID controller parameters for the fired heater at the lower operating condition using the transfer function (1.58) and simulate the closed-loop response with a step reference signal using sampling interval (min) and a negative step disturbance entering at the half of the simulation time.
The higher operating condition case is left as an exercise.
Solution. Figure 1.21 shows the unit step response with the lines drawn to identify the time delay and time constant for a first order approximation. From the graph, the time delay is found as 9.54 min and the time constant min. With the steady-state gain equal to 3, the approximation using first order plus model leads to the following transfer function:
(1.60) 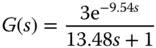
Now, applying the Ziegler–Nichols tuning rules (see Table 1.2), Cohen–Coon tuning rules (see Table 1.3) and Wang–Cluett tuning rules (see Table 1.6), we obtain the PI controller parameters for the fired heater process shown in Table 1.9. The PI controller parameters obtained are drastically different. The PI controllers using Ziegler–Nichols and Wang–Cluett tuning rules produce stable closed-loop system for the fired heater process, however the PI controller using Cohen–Coon tuning rules does not lead to a stable closed-loop system, which was verified using closed-loop simulation. To evaluate the closed-loop control performance, a unit step input signal is used as a reference and a step input disturbance with magnitude of is added to the closed-loop simulation at half of the simulation time. Figure 1.22(a) shows the control signals generated by the PI controllers and Figure 1.22(b) shows the output responses to the reference change and the disturbance signal. Both closed-loop systems have oscillations, but in comparison, the controller using Wang–Cluett tuning rules leads to a slightly better closed-loop performance with less oscillations.
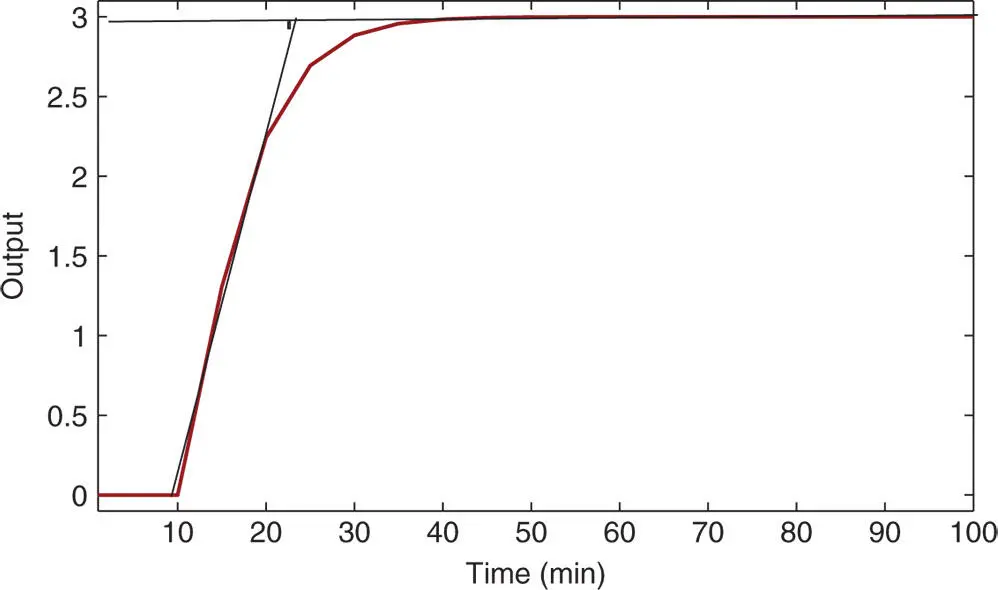
Figure 1.21Unit step response of the fired heater process.
Table 1.9PI controller parameters with reaction curve.
|
|
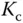 |
|
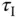 |
| Ziegler–Nichols |
|
0.4239 |
|
28.6200 |
| Cohen–Coon |
|
0.4517 |
|
13.2353 |
| Wang–Cluett |
|
0.2835 |
|
15.7610 |
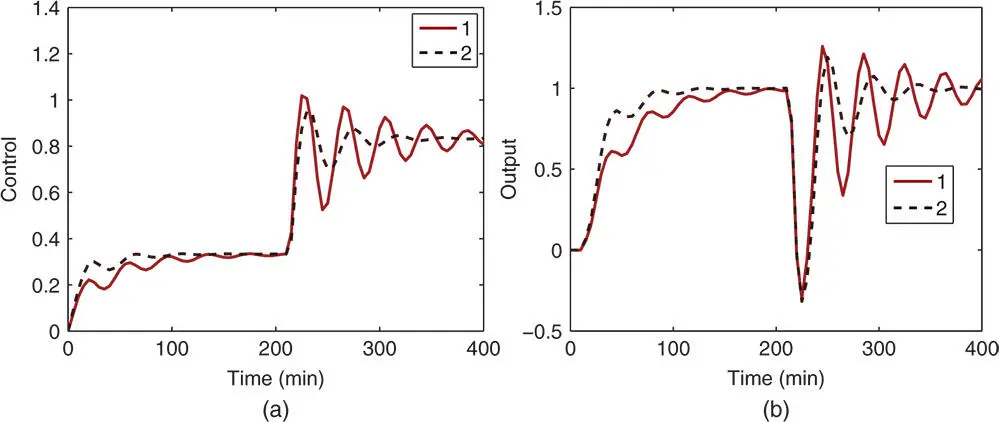
Figure 1.22Comparison of closed-loop responses using Ziegler–Nichols and Wang–Cluett tuning rules ( Example 1.9). (a) Control signal. (b) Output. Key: line (1) Ziegler–Nichols tuning rule; line (2) Wang–Cluett tuning rule.
Читать дальше


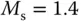 ; line (2) tuning rule with
; line (2) tuning rule with 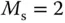 .
.
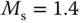 ; line (2) tuning rule with
; line (2) tuning rule with 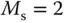 .
.