4 Chapter 5Table 5.1 Properties represented by second‐rank tensors.Table 5.2 Number of independent components of physical properties represented...
5 Chapter 6Table 6.1 Elastic constants of cubic crystals at room temperatureTable 6.2 Forms of the compliance and stiffness constant arraysTable 6.3 The equations giving the compliances s ijin terms of the stiffness c...Table 6.4 Elastic constants of hexagonal crystals at room temperature; x 3‐axis...Table 6.5 Forms of the compliance and stiffness constant arrays for the diffe...
6 Chapter 7Table 7.1 Glide elements of crystals (at room temperature and at atmospheric ...Table 7.2 Predominant slip planes for h.c.p. metals at room temperature. In e...Table 7.3 Independent slip systems in crystalsTable 7.4 The six slip systems in crystals with the NaCl structure, labelled ...
7 Chapter 9Table 9.1 Definitely stable dislocations in some Bravais latticesTable 9.2 The stacking fault energies of c.c.p. metalsTable 9.3 Dislocations in c.c.p. metals
8 Chapter 10Table 10.1 Estimated number of jumps made per second by a point defect having...Table 10.2 Relaxation displacements around a vacancy expressed as a percentag...Table 10.3 Fraction of sites vacant at the melting point, n / N , in equilibrium...Table 10.4 Energies of formation and migration of vacancy defects in metals, E
9 Chapter 11Table 11.1 The twinning elements of various crystals
10 Chapter 13Table 13.1 Surface free energies of solidsTable 13.2 Some coincidence lattices for c.c.p. and b.c.c. crystals [20]Table 13.3 Disorientation descriptions for compound twins in h.c.p. metalsTable 13.4 Experimentally determined energies of high‐angle grain boundariesTable 13.5 Twin boundary free energies, γ T, relative to surface energies,...
11 Chapter 14Table 14.1 Relative energies of random interphase boundariesTable 14.2 Epitaxial deposition of c.c.p. metals. (After [7].)Table 14.3 Lattice parameters and stiffness constants for some common semicon...
12 Chapter 15Table 15.1 Some common end or final textures
13 5Table A5.1 The twelve slip systems in c.c.p. metal crystals, labelled here fo...Table A5.2 Slip systems and their corresponding Schmid factors in c.c.p. meta...
1 Chapter 1 Figure 1.1 (a) The arrangement of the atoms in graphene, a single sheet of g... Figure 1.2 Definition of the smallest separations a , b and c of the lattice ... Figure 1.3 The numbers give the elevations of the centres of the atoms, alon... Figure 1.4 A rectangular mesh of a hypothetical two‐dimensional crystal with... Figure 1.5 Demonstration of the law of constancy of angles between faces of ... Figure 1.6 A vector rwritten as the sum of translations along the x ‐, y ‐ an... Figure 1.7 Examples of various lattice vectors in a crystal Figure 1.8 The plane ( hkl ) in a crystal making intercepts of a/ h , b/ k and c/ Figure 1.9 Examples of various lattice planes in a crystal. The indices of t... Figure 1.10 The plane ( hkl ) in a crystal making intercepts of a/ h , b/ k and c Figure 1.11 Translation symmetry in a crystal Figure 1.12 Reflection symmetry Figure 1.13 Diagram to help determine which rotation axes are consistent wit... Figure 1.14 The five symmetrical plane lattices or nets. Rotational symmetry... Figure 1.15 Restrictions placed on two‐dimensional lattices through the impo... Figure 1.16 The two possible arrangements of nets consistent with mirror sym... Figure 1.17 Examples of possible allowed combinations of rotational symmetri... Figure 1.18 Stacking of nets to build up a space lattice. The triplet of vec... Figure 1.19 Unit cells of the 14 Bravais space lattices. (a) Primitive tricl... Figure 1.20 Lattice points in the net at height zero are marked as dots, tho... Figure 1.21 A three‐dimensional view of the staggered arrangement of nets in... Figure 1.22 Lattice points in the net at height zero are marked with dots. T... Figure 1.23 The stacking of rhombus nets vertically above one another to for... Figure 1.24 The three possible stacking sequences of rectangular nets. In th... Figure 1.25 The staggered stacking of rhombus nets. This form of stacking ge... Figure 1.26 The stacking of triequiangular nets of points in a staggered seq... Figure 1.27 Lattice points in the net at level zero are marked with a dot, t... Figure 1.28 The relationship between a primitive cell of the trigonal lattic... Figure 1.29 Plan view of the alternative triply primitive hexagonal unit cel... Figure 1.30 The four 〈111〉 three‐fold axes with acute angles of 70.53° betwe... Figure 1.31 The relationship between the primitive unit cell and the convent... Figure 1.32 The relationship between the primitive unit cell and the convent...
2 Chapter 2 Figure 2.1 The basic operation of repetition by a rotation axis. In this exa... Figure 2.2 Stereograms representing the operation of one‐, two‐, three‐, fou... Figure 2.3 The repetition of an object by a mirror plane, (a) and (b), and b... Figure 2.4 The operation of the twofold rotoinversion axis, 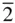 Figure 2.5 The operation of the various rotoinversion axes that can occur in... Figure 2.6 Stereograms of the poles of equivalent general directions and of ... Figure 2.7 A stereogram of an orthorhombic crystal of point group 222 centre... Figure 2.8 (a) General location of a hk 0 pole on the stereogram of an orthor... Figure 2.9 The cubic point group of lowest symmetry: 23 Figure 2.10 Stereograms centred on 001 of (a) mirror planes parallel to {100... Figure 2.11 Stereogram of a cubic crystal. Figure 2.12 (a) Stereogram of the holosymmetric class of the hexagonal syste... Figure 2.13 Geometry to show that in Miller−Bravais indices ( hkil ), i = −( h ... Figure 2.14 Indices of various directions in the hexagonal system specified ... Figure 2.15 Geometry to determine the angle θ between the (0001) pole a... Figure 2.16 A stereogram of a trigonal crystal of class
Figure 2.5 The operation of the various rotoinversion axes that can occur in... Figure 2.6 Stereograms of the poles of equivalent general directions and of ... Figure 2.7 A stereogram of an orthorhombic crystal of point group 222 centre... Figure 2.8 (a) General location of a hk 0 pole on the stereogram of an orthor... Figure 2.9 The cubic point group of lowest symmetry: 23 Figure 2.10 Stereograms centred on 001 of (a) mirror planes parallel to {100... Figure 2.11 Stereogram of a cubic crystal. Figure 2.12 (a) Stereogram of the holosymmetric class of the hexagonal syste... Figure 2.13 Geometry to show that in Miller−Bravais indices ( hkil ), i = −( h ... Figure 2.14 Indices of various directions in the hexagonal system specified ... Figure 2.15 Geometry to determine the angle θ between the (0001) pole a... Figure 2.16 A stereogram of a trigonal crystal of class 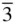 m with a rhombohedr... Figure 2.17 The same crystal as in Figure 2.16 indexed using a hexagonal cel... Figure 2.18 The relationship between the special forms {10
m with a rhombohedr... Figure 2.17 The same crystal as in Figure 2.16 indexed using a hexagonal cel... Figure 2.18 The relationship between the special forms {10  1} and {01
1} and {01 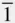 1} in ... Figure 2.19 Monoclinic stereogram centred on [001] for the 2nd setting Figure 2.20 A diagram from which the angle φ in Figure 2.19 between 010... Figure 2.21 Diagrams relevant to drawing stereograms of triclinic crystals. ... Figure 2.22 (a) A twofold rotation axis. (b) A 2 1screw axis. (c) A glide pl... Figure 2.23 Screw axes 3 1and 3 2: these are screw axes of opposite hand, as ... Figure 2.24 The 17 two‐dimensional space groups arranged following the Inter ... Figure 2.25 An example of a space group. Figure 2.26 The 10 black‐and‐white plane lattices: (a) parallelogram (obliqu... Figure 2.27 The effect of antiferromagnetic coupling on the size of the unit...
1} in ... Figure 2.19 Monoclinic stereogram centred on [001] for the 2nd setting Figure 2.20 A diagram from which the angle φ in Figure 2.19 between 010... Figure 2.21 Diagrams relevant to drawing stereograms of triclinic crystals. ... Figure 2.22 (a) A twofold rotation axis. (b) A 2 1screw axis. (c) A glide pl... Figure 2.23 Screw axes 3 1and 3 2: these are screw axes of opposite hand, as ... Figure 2.24 The 17 two‐dimensional space groups arranged following the Inter ... Figure 2.25 An example of a space group. Figure 2.26 The 10 black‐and‐white plane lattices: (a) parallelogram (obliqu... Figure 2.27 The effect of antiferromagnetic coupling on the size of the unit...
3 Chapter 3 Figure 3.1 (a) The conventional unit cell of the c.c.p. crystal structure. (... Figure 3.2 Close packing of equal spheres. (a) Cubic close‐packed (c.c.p.). ... Figure 3.3 Plan view of the ABCABCABC… stacking sequence of (111) planes in ... Figure 3.4 The stacking of closest‐packed planes in (a) the c.c.p. structure... Figure 3.5 The largest interstice in the c.c.p. structure: the octahedral in... Figure 3.6 The second largest interstice in the c.c.p. structure: the tetrah... Figure 3.7 The unit cell of the h.c.p. structure Figure 3.8 Interstices in the h.c.p. arrangement. The octahedral interstices... Figure 3.9 The b.c.c crystal structure Figure 3.10 Tetrahedral ( X ) and octahedral ( O ) interstices in the b.c.c crys... Figure 3.11 The crystal structure of mercury, showing the primitive rhombohe... Figure 3.12 The crystal structure of diamond Figure 3.13 The stacking of (111) planes in the diamond and sphalerite struc... Figure 3.14 (a) The crystal structure of graphite. (b) The crystal structure... Figure 3.15 The crystal structure of As, Sb and BiFigure 3.16 The crystal structure of sodium chloride, NaClFigure 3.17 The crystal structure of caesium chloride, CsClFigure 3.18 The crystal structures of (a) sphalerite ( α ‐ZnS) and (b) wu...Figure 3.19 The crystal structure of nickel arsenide, NiAsFigure 3.20 The crystal structure of calcium fluoride, CaF 2Figure 3.21 (a) The crystal structure of rutile, TiO 2. (b) The rutile crysta...Figure 3.22 The crystal structure of perovskite, Pm 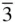 m Figure 3.23 The structure of sapphire ( α ‐Al 2O 3or corundum). The large ...Figure 3.24 One‐eighth of the unit cell of spinel, MgAl 2O 4Figure 3.25 Coordination about the oxygen ions (solid black circles) in a ga...Figure 3.26 The structure of calcite (CaCO 3). The primitive rhombohedral uni...Figure 3.27 A c.c.p. crystal showing (a) a substitutional solid solution and...Figure 3.28 (a) A (111) plane of the disordered form of Cu 3Au. (b) A (111) p...Figure 3.29 Structures of ordered solid solutions: (a) B 2, (b) D 0 3, (c) D 0 19Figure 3.30 Molecular models of (a) polyethylene (–CH 2–) nand (b) polytetraf...Figure 3.31 (a) Unit cell of polyethylene viewed along [001]. The unit cell ...Figure 3.32 Illustration of a continuous polymer chain running through neigh...
m Figure 3.23 The structure of sapphire ( α ‐Al 2O 3or corundum). The large ...Figure 3.24 One‐eighth of the unit cell of spinel, MgAl 2O 4Figure 3.25 Coordination about the oxygen ions (solid black circles) in a ga...Figure 3.26 The structure of calcite (CaCO 3). The primitive rhombohedral uni...Figure 3.27 A c.c.p. crystal showing (a) a substitutional solid solution and...Figure 3.28 (a) A (111) plane of the disordered form of Cu 3Au. (b) A (111) p...Figure 3.29 Structures of ordered solid solutions: (a) B 2, (b) D 0 3, (c) D 0 19Figure 3.30 Molecular models of (a) polyethylene (–CH 2–) nand (b) polytetraf...Figure 3.31 (a) Unit cell of polyethylene viewed along [001]. The unit cell ...Figure 3.32 Illustration of a continuous polymer chain running through neigh...
Читать дальше

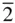 Figure 2.5 The operation of the various rotoinversion axes that can occur in... Figure 2.6 Stereograms of the poles of equivalent general directions and of ... Figure 2.7 A stereogram of an orthorhombic crystal of point group 222 centre... Figure 2.8 (a) General location of a hk 0 pole on the stereogram of an orthor... Figure 2.9 The cubic point group of lowest symmetry: 23 Figure 2.10 Stereograms centred on 001 of (a) mirror planes parallel to {100... Figure 2.11 Stereogram of a cubic crystal. Figure 2.12 (a) Stereogram of the holosymmetric class of the hexagonal syste... Figure 2.13 Geometry to show that in Miller−Bravais indices ( hkil ), i = −( h ... Figure 2.14 Indices of various directions in the hexagonal system specified ... Figure 2.15 Geometry to determine the angle θ between the (0001) pole a... Figure 2.16 A stereogram of a trigonal crystal of class
Figure 2.5 The operation of the various rotoinversion axes that can occur in... Figure 2.6 Stereograms of the poles of equivalent general directions and of ... Figure 2.7 A stereogram of an orthorhombic crystal of point group 222 centre... Figure 2.8 (a) General location of a hk 0 pole on the stereogram of an orthor... Figure 2.9 The cubic point group of lowest symmetry: 23 Figure 2.10 Stereograms centred on 001 of (a) mirror planes parallel to {100... Figure 2.11 Stereogram of a cubic crystal. Figure 2.12 (a) Stereogram of the holosymmetric class of the hexagonal syste... Figure 2.13 Geometry to show that in Miller−Bravais indices ( hkil ), i = −( h ... Figure 2.14 Indices of various directions in the hexagonal system specified ... Figure 2.15 Geometry to determine the angle θ between the (0001) pole a... Figure 2.16 A stereogram of a trigonal crystal of class 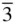 m with a rhombohedr... Figure 2.17 The same crystal as in Figure 2.16 indexed using a hexagonal cel... Figure 2.18 The relationship between the special forms {10
m with a rhombohedr... Figure 2.17 The same crystal as in Figure 2.16 indexed using a hexagonal cel... Figure 2.18 The relationship between the special forms {10  1} and {01
1} and {01 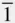 1} in ... Figure 2.19 Monoclinic stereogram centred on [001] for the 2nd setting Figure 2.20 A diagram from which the angle φ in Figure 2.19 between 010... Figure 2.21 Diagrams relevant to drawing stereograms of triclinic crystals. ... Figure 2.22 (a) A twofold rotation axis. (b) A 2 1screw axis. (c) A glide pl... Figure 2.23 Screw axes 3 1and 3 2: these are screw axes of opposite hand, as ... Figure 2.24 The 17 two‐dimensional space groups arranged following the Inter ... Figure 2.25 An example of a space group. Figure 2.26 The 10 black‐and‐white plane lattices: (a) parallelogram (obliqu... Figure 2.27 The effect of antiferromagnetic coupling on the size of the unit...
1} in ... Figure 2.19 Monoclinic stereogram centred on [001] for the 2nd setting Figure 2.20 A diagram from which the angle φ in Figure 2.19 between 010... Figure 2.21 Diagrams relevant to drawing stereograms of triclinic crystals. ... Figure 2.22 (a) A twofold rotation axis. (b) A 2 1screw axis. (c) A glide pl... Figure 2.23 Screw axes 3 1and 3 2: these are screw axes of opposite hand, as ... Figure 2.24 The 17 two‐dimensional space groups arranged following the Inter ... Figure 2.25 An example of a space group. Figure 2.26 The 10 black‐and‐white plane lattices: (a) parallelogram (obliqu... Figure 2.27 The effect of antiferromagnetic coupling on the size of the unit...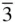 m Figure 3.23 The structure of sapphire ( α ‐Al 2O 3or corundum). The large ...Figure 3.24 One‐eighth of the unit cell of spinel, MgAl 2O 4Figure 3.25 Coordination about the oxygen ions (solid black circles) in a ga...Figure 3.26 The structure of calcite (CaCO 3). The primitive rhombohedral uni...Figure 3.27 A c.c.p. crystal showing (a) a substitutional solid solution and...Figure 3.28 (a) A (111) plane of the disordered form of Cu 3Au. (b) A (111) p...Figure 3.29 Structures of ordered solid solutions: (a) B 2, (b) D 0 3, (c) D 0 19Figure 3.30 Molecular models of (a) polyethylene (–CH 2–) nand (b) polytetraf...Figure 3.31 (a) Unit cell of polyethylene viewed along [001]. The unit cell ...Figure 3.32 Illustration of a continuous polymer chain running through neigh...
m Figure 3.23 The structure of sapphire ( α ‐Al 2O 3or corundum). The large ...Figure 3.24 One‐eighth of the unit cell of spinel, MgAl 2O 4Figure 3.25 Coordination about the oxygen ions (solid black circles) in a ga...Figure 3.26 The structure of calcite (CaCO 3). The primitive rhombohedral uni...Figure 3.27 A c.c.p. crystal showing (a) a substitutional solid solution and...Figure 3.28 (a) A (111) plane of the disordered form of Cu 3Au. (b) A (111) p...Figure 3.29 Structures of ordered solid solutions: (a) B 2, (b) D 0 3, (c) D 0 19Figure 3.30 Molecular models of (a) polyethylene (–CH 2–) nand (b) polytetraf...Figure 3.31 (a) Unit cell of polyethylene viewed along [001]. The unit cell ...Figure 3.32 Illustration of a continuous polymer chain running through neigh...










