1 ...7 8 9 11 12 13 ...16 Sharpe also saw that investors often held cash, and cash did not fit readily into the world of risky assets that Markowitz outlined. Cash might sit in a drawer or a bank account or a Treasury bill and offer an unvarying return over an investor's time horizon, a return uncorrelated with returns from riskier assets. He also saw that investors could borrow cash and invest in risky assets. Cash and similar riskless assets had a special role to play.
Sharpe adapted an idea originally described by James Tobin at Yale and assumed that all investors could borrow or lend money at a single, common riskless rate (Tobin, 1958). Individuals, corporations, and even the US Treasury would pay the same rate of interest. This is not as unrealistic as it might sound at first. Once individuals or corporations put up valuable property or other collateral to secure a loan, interest rates can vary by only a small amount at least over short periods.
Sharpe knew he would be challenged. “These are highly restrictive and undoubtedly unrealistic assumptions,” he noted. But he argued that the implications of his approach fit beautifully with some of the key predictions of classical finance. Beauty in theory would win over beauty in practice.
The immediate implication of holding cash or lending at a common riskless rate along with a common view of risky assets would be that an investor could hold a mix of cash and risky assets. If the investor held only cash, the portfolio would spin off a riskless return. If the investor held only efficient risky assets, the portfolio would spin off a return somewhere along the efficient frontier. If the investor held a mix of cash and risky assets, returns would fall somewhere along a line between a riskless return and a single point on the efficient frontier.
If the investor then went a step further and borrowed money to buy an efficient portfolio of risky assets, the line would extend beyond the efficient frontier. This was a striking idea. If an investor borrowed enough to double the size of the investment in the efficient portfolio of risky assets, the resulting leveraged portfolio would have a multiple of the expected return and risk. The line would start at the riskless asset, touch a portfolio on the efficient frontier, and keep going from there ( figure 2.2). This was Sharpe's transformational idea of the capital market line. This line represents all combinations of the riskless asset and a risky portfolio. The investor could hold only the riskless asset, only the risky portfolio, or all combinations in between. If the investor borrowed money and used it to buy more of the risky portfolio, then investors would hold more than one times their money in the risky portfolio and the capital market line would keep on going.
Sharpe's capital market line had a remarkable feature: for any level of risk, it offered an equal or higher expected return than any point along the efficient frontier. And for any level of return, the capital market line offered equal or lower risk than the efficient frontier. Sharpe had found a solution to choosing from the infinite investment list that was better and simpler than Markowitz. Rather than settling along the efficient frontier, an investor instead should buy the risky portfolio when the capital market line touches the efficient frontier and then combine that portfolio with borrowing or lending at the riskless rate. Portfolios along the capital market line offer a better result than anything the investor could find along the efficient frontier.
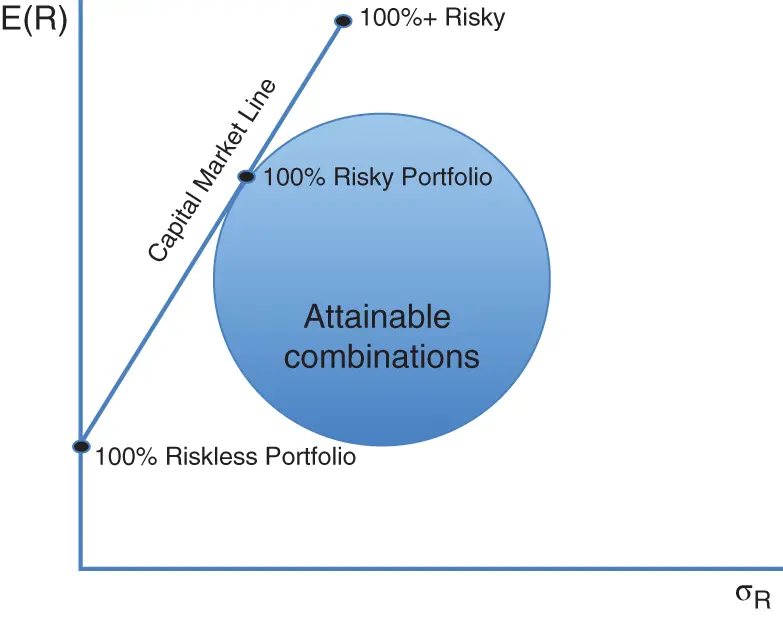
Figure 2.2 Borrowing and lending at the riskless rate allows any investor to hold a combination of a riskless and risky asset, which Sharpe dubbed the capital market line.
Sharpe's capital market line reduced the complexity of Markowitz's approach. With a common view of asset performance, investors all should buy the same market portfolio of risky assets and individually either blend it with a relatively riskless investment or borrow and buy more of the portfolio to suit preferences for risk and return.
The complexity of the infinite investment menu had moved from the search for the single best investment through Markowitz to the efficient frontier and now through Sharpe to the capital market line. Investing had been reduced to a simple decision about the best mix of cash, borrowing, and a single efficient risk portfolio.
Putting a Price on Assets Along the Capital Market Line
Sharpe's approach also led to another powerful conclusion about the value of available investable assets, a conclusion that ever since has broadly set the terms for evaluating assets and investment managers.
Sharpe noted that if every investor decided to invest at least partially in the same risky portfolio, then the assets included in that portfolio would rise in value. A higher price would mean a decline in potential return compared to assets outside the initial portfolio. The assets outside the initial portfolio would become more attractive, and investors would look for portfolios that included the previously excluded assets. The value of those assets would rise until they aligned with the value of the initial portfolio, and investors' search for the next margin of excluded assets would continue. The value of included and excluded assets would continue to change until all assets had a place in at least one portfolio that lay along the capital market line—portfolios that promised a constant extra measure of return for each extra measure of risk ( figure 2.3). Not all portfolios would have to include the same assets, but all portfolios would offer a combination of risk and return that matched at least one possibility along the line. And all portfolios along the capital market line would produce returns perfectly correlated with one another.
Sharpe then made the case that the value of any investment depends only on the amount of risk the asset shares with portfolios along the capital market line. Think of that as the risk of overall economic growth or decline. The remaining risk in an asset was unique or idiosyncratic. It could reflect the unpredictable effects of personnel or reputation or local markets or other factors. By combining investments, a portfolio could balance bad luck on one investment with good luck on another, just like the effect of flipping multiple coins can balance out into a smooth set of outcomes. But the core, systematic risk in an investment an investor cannot diversify away. And if the investor cannot eliminate the risk, then the investor needs fair compensation.
The expected return on any specific asset, according to Sharpe, reflects the expected return on the riskless asset, the expected return on the market portfolio of risky assets, and the proportion of risk that the specific asset shares with the market portfolio. In the world of CAPM, the expected return on a specific asset becomes 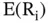 . The expected return on the riskless asset becomes
. The expected return on the riskless asset becomes 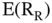 . The return on the market portfolio becomes
. The return on the market portfolio becomes 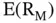 , and the excess return on the market portfolio above the riskless return becomes
, and the excess return on the market portfolio above the riskless return becomes 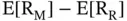 . Finally, the excess return on the market portfolio is multiplied by a number,
. Finally, the excess return on the market portfolio is multiplied by a number, 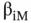 , or beta, which indicates whether the specific asset is more or less risky than the market portfolio overall. 1 If the asset is more risky, beta is greater than 1; if it is less risky, beta is smaller than 1. All of these pieces fit together in a simple equation that revolutionized finance in the same way that Einstein's equation revolutionized physics:
, or beta, which indicates whether the specific asset is more or less risky than the market portfolio overall. 1 If the asset is more risky, beta is greater than 1; if it is less risky, beta is smaller than 1. All of these pieces fit together in a simple equation that revolutionized finance in the same way that Einstein's equation revolutionized physics:
Читать дальше


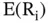 . The expected return on the riskless asset becomes
. The expected return on the riskless asset becomes 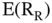 . The return on the market portfolio becomes
. The return on the market portfolio becomes 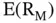 , and the excess return on the market portfolio above the riskless return becomes
, and the excess return on the market portfolio above the riskless return becomes 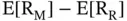 . Finally, the excess return on the market portfolio is multiplied by a number,
. Finally, the excess return on the market portfolio is multiplied by a number, 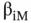 , or beta, which indicates whether the specific asset is more or less risky than the market portfolio overall. 1 If the asset is more risky, beta is greater than 1; if it is less risky, beta is smaller than 1. All of these pieces fit together in a simple equation that revolutionized finance in the same way that Einstein's equation revolutionized physics:
, or beta, which indicates whether the specific asset is more or less risky than the market portfolio overall. 1 If the asset is more risky, beta is greater than 1; if it is less risky, beta is smaller than 1. All of these pieces fit together in a simple equation that revolutionized finance in the same way that Einstein's equation revolutionized physics:










