Steven Abrahams - Competitive Advantage in Investing

2 2If the real rate of interest over 10 years is 2.5% and the investor's cost of living goes up 2.5% a year, then a stream of annual $1 dividends is worth only $7.72 today: . If the investor worries that the company paying the $1 every year could go out of business, the investor might need something extra to compensate for the risk, say another 2.5% a year, then the stream of dividends is worth only $6.86 today: . Alternatively, the riskier company could compensate a nervous investor by paying more than $1 a year, in fact, exactly 12.5 cents more a year:

3 3Variance is a measure of dispersion around an average. Variance in returns over a series of investment periods would be measured as Variance of Returns = ∑ (Return over period t – Average over all periods)2/(Total number of periods – 1).

4 4For an investment that pays discrete cash flows, xi, with a certain probability, pi, where .

5 5The expected return for a simple portfolio of two securities is , where and are the expected returns on investment A and investment B and and are the percent of the portfolio in investment A and investment B . Markowitz assumed and add to 100% and the investor could not sell either investment short, in other words, that . The variance of a portfolio with two securities is or, more intuitively, . In the latter expression, is the variance of returns on investment A, for instance, and is the correlation between returns on investments A and B. The latter expression for portfolio variance or risk shows more clearly that risk drops as the correlation between the two securities, , drops below 1 or even goes negative. This is the formal expression for the impact of diversification.

6 6This idea, too, can have a formal representation for a set of assets, A, B, and C, and a set of risk factors, N, M, and P: Assets with sensitivity to different risksRisk factorAssetNMPABCThe return on each asset depends on a common risk factor N, the return on assets B and C depend on factor M, and the return of asset C only depends on factor P. And each asset has a different sensitivity to its underlying risk factors.Any asset is a combination of exposures to a wide range of underlying risks. In other words, an asset itself is already a portfolio—a portfolio of risk exposures. And those risk exposures can change over time. The variance of any asset at any point in time depends on both the sensitivity to each underlying risk and the variance in each underlying risk. For an asset sensitive to two latent factors:where is the variance of return on the assetis the variance of factor n is the variance of factor m is the covariance between factors n and mThe correlation between assets depends on shared risk dimensions, correlated risk dimensions, and sensitivity to the underlying risks. For a pair of assets, A and B, that both depend on the influence of two risk dimensions, N and M, their returns look as follows:It is easy to show thatThis means that the covariance between A and B depends on their respective sensitivity to the underlying risk dimensions. If the investor changes that sensitivity through hedging, for instance, the covariance between the assets will change. Consequently, the diversifying effect of the assets in a mean-variance portfolio also will change.Changing asset exposure to underlying risk dimensions means that investors can manage the correlation between two assets. The ability to hedge or offset some or all dimensions of risk embedded in an asset allows an investor to choose the amount of variance and correlation in and between assets. Take the example where an investor takes a long position in A and a short position in B:The resulting risk combination differs from both A and B. The new combination will have a unique correlation to A, B, and to other assets.Once an investor breaks an asset down into underlying exposures, applying Markowitz's framework involves even more judgment about expected return, variance, and correlation. Portfolios that include hedges or short positions further open the possibility of competitive advantage because investors can exclude risks where they might have disadvantage and emphasize ones where they have advantage.

Although Markowitz in 1952 drew the map of the efficient frontier, he still left it up to each investor to find the best place to settle. Some places along the frontier offered low risk and low reward, some high risk and high reward, and some a Goldilocks combination. To each, his or her own.

Markowitz's only advice was to ask for more return with each extra measure of risk taken. Investors should not take risk for free. An investor might put money in a drawer and get just enough return to protect against inflation. But as risk goes up, so should the required return. The amount of additional return might differ for each investor. The adventurous might require a little, the cautious a lot. Markowitz does not prescribe the trade-off.

Markowitz does describe investors as risk averse, meaning not that investors avoid risk but only that investors need more return to compensate for more risk. As risk rises, so does required return. The trade-off that each investor makes between risk and return creates a map of the investor's preferences. A line on that map might start at the point of no risk and return and slope gently or sharply upwards, or it might curve up like an airplane lifting off a runway. For the same level of risk, of course, the investor would take the highest return. That moves the line or the curve up to a higher starting point.

An investor's map of preferred investment risk and return can help the investor or the investor's advisor find a place along the efficient frontier. One line in that map should intersect with the combinations of risk and return that are available along the efficient frontier ( figure 2.1). Preference meets reality. At that intersection, Markowitz advised, invest.

Markowitz's advice still left investors with a lot of work to do. Each investor had to figure out risk, return, and correlation of each investment on the infinite list. That led to each investor's own efficient frontier. And the investor still had to figure out the map of risk and return preferences and where those might line up with the investor's own efficient frontier.

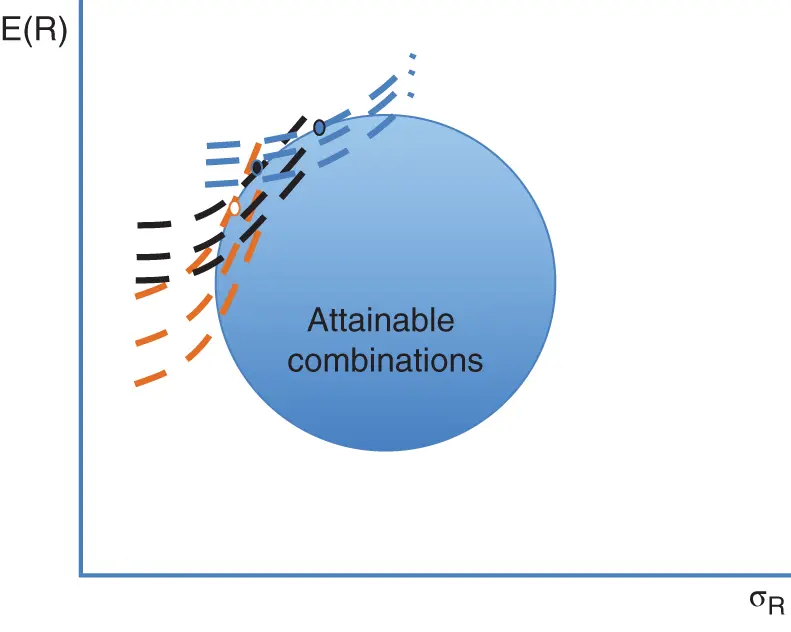
Figure 2.1 In Markowitz's world, every risk-averse investor would make a different trade-off between extra risk and extra return and choose a different portfolio.

Markowitz had changed the state of the investment art, but a simple guide to using it would have to wait at least another 10 years.

William Sharpe at Stanford and later John Lintner at Harvard separately came along more than a decade later and built on Markowitz's approach (Sharpe, 1964; Lintner, 1965). They developed a method that not only had something to say about the best way to combine all the items on the infinite investment list and choose a single best portfolio but also had something to say about how much each investment was worth. Known today as the capital asset pricing model, or CAPM, it probably has become the most broadly taught framework for building a portfolio and for valuing the assets that go into it. It has also led to important tools for measuring the important costs of running a company and for gauging the performance of asset managers. And, like all good theories, it was beautifully simple. Perhaps too beautiful.

To Markowitz's framework, Sharpe added the assumption that all investors agree on the most important features of asset returns over a given investment horizon: their likely mean, variance, and correlation. Investors see the same security cash flows, the same risk attributes driving those cash flows, and the same future path for those risks. All investors see the same world of possible investments. Most important, all investors see the same efficient frontier. He might have argued that investors can all have different opinions about given investments, but they can't have their own facts. Common facts prevail.