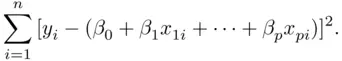1 1.1 Introduction
2 1.2 Concepts and Background Material 1.2.1The Linear Regression Model 1.2.2Estimation Using Least Squares 1.2.3Assumptions
3 1.3 Methodology 1.3.1Interpreting Regression Coefficients 1.3.2Measuring the Strength of the Regression Relationship 1.3.3Hypothesis Tests and Confidence Intervals for β 1.3.4Fitted Values and Predictions 1.3.5Checking Assumptions Using Residual Plots
4 1.4 Example—Estimating Home Prices
5 1.5 Summary
This is a book about regression modeling, but when we refer to regression models, what do we mean? The regression framework can be characterized in the following way:
1 We have one particular variable that we are interested in understanding or modeling, such as sales of a particular product, sale price of a home, or voting preference of a particular voter. This variable is called the target, response, or dependent variable, and is usually represented by .
2 We have a set of other variables that we think might be useful in predicting or modeling the target variable (the price of the product, the competitor's price, and so on; or the lot size, number of bedrooms, number of bathrooms of the home, and so on; or the gender, age, income, party membership of the voter, and so on). These are called the predicting, or independent variables, and are usually represented by , , etc.
Typically, a regression analysis is used for one (or more) of three purposes:
1 modeling the relationship between and ;
2 prediction of the target variable (forecasting);
3 and testing of hypotheses.
In this chapter, we introduce the basic multiple linear regression model, and discuss how this model can be used for these three purposes. Specifically, we discuss the interpretations of the estimates of different regression parameters, the assumptions underlying the model, measures of the strength of the relationship between the target and predictor variables, the construction of tests of hypotheses and intervals related to regression parameters, and the checking of assumptions using diagnostic plots.
1.2 Concepts and Background Material
1.2.1 THE LINEAR REGRESSION MODEL
The data consist of 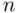 observations, which are sets of observed values
observations, which are sets of observed values 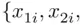
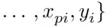 that represent a random sample from a larger population. It is assumed that these observations satisfy a linear relationship,
that represent a random sample from a larger population. It is assumed that these observations satisfy a linear relationship,
(1.1) 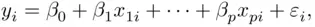
where the 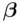 coefficients are unknown parameters, and the
coefficients are unknown parameters, and the  are random error terms. By a linear model, it is meant that the model is linear in the parameters ; a quadratic model,
are random error terms. By a linear model, it is meant that the model is linear in the parameters ; a quadratic model,
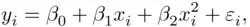
paradoxically enough, is a linear model, since 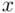 and
and 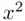 are just versions of
are just versions of 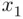 and
and 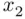 .
.
It is important to recognize that this, or any statistical model, is not viewed as a true representation of reality; rather, the goal is that the model be a useful representation of reality. A model can be used to explore the relationships between variables and make accurate forecasts based on those relationships even if it is not the “truth.” Further, any statistical model is only temporary, representing a provisional version of views about the random process being studied. Models can, and should, change, based on analysis using the current model, selection among several candidate models, the acquisition of new data, new understanding of the underlying random process, and so on. Further, it is often the case that there are several different models that are reasonable representations of reality. Having said this, we will sometimes refer to the “true” model, but this should be understood as referring to the underlying form of the currently hypothesized representation of the regression relationship.
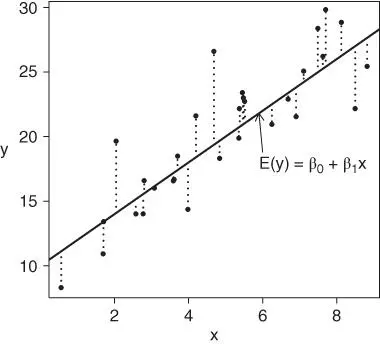
FIGURE 1.1: The simple linear regression model. The solid line corresponds to the true regression line, and the dotted lines correspond to the random errors 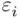 .
.
The special case of (1.1)with 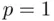 corresponds to the simple regression model, and is consistent with the representation in Figure 1.1. The solid line is the true regression line, the expected value of
corresponds to the simple regression model, and is consistent with the representation in Figure 1.1. The solid line is the true regression line, the expected value of 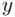 given the value of
given the value of 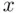 . The dotted lines are the random errors
. The dotted lines are the random errors 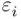 that account for the lack of a perfect association between the predictor and the target variables.
that account for the lack of a perfect association between the predictor and the target variables.
1.2.2 ESTIMATION USING LEAST SQUARES
The true regression function represents the expected relationship between the target and the predictor variables, which is unknown. A primary goal of a regression analysis is to estimate this relationship, or equivalently, to estimate the unknown parameters 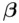 . This requires a data‐based rule, or criterion, that will give a reasonable estimate. The standard approach is least squares regression, where the estimates are chosen to minimize
. This requires a data‐based rule, or criterion, that will give a reasonable estimate. The standard approach is least squares regression, where the estimates are chosen to minimize
(1.2) 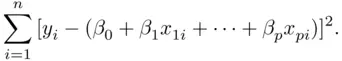
Читать дальше

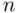 observations, which are sets of observed values
observations, which are sets of observed values 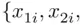
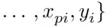 that represent a random sample from a larger population. It is assumed that these observations satisfy a linear relationship,
that represent a random sample from a larger population. It is assumed that these observations satisfy a linear relationship,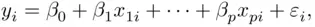
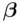 coefficients are unknown parameters, and the
coefficients are unknown parameters, and the  are random error terms. By a linear model, it is meant that the model is linear in the parameters ; a quadratic model,
are random error terms. By a linear model, it is meant that the model is linear in the parameters ; a quadratic model,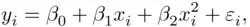
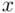 and
and 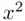 are just versions of
are just versions of 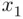 and
and 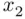 .
.
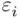 .
.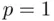 corresponds to the simple regression model, and is consistent with the representation in Figure 1.1. The solid line is the true regression line, the expected value of
corresponds to the simple regression model, and is consistent with the representation in Figure 1.1. The solid line is the true regression line, the expected value of 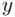 given the value of
given the value of 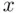 . The dotted lines are the random errors
. The dotted lines are the random errors 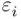 that account for the lack of a perfect association between the predictor and the target variables.
that account for the lack of a perfect association between the predictor and the target variables.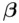 . This requires a data‐based rule, or criterion, that will give a reasonable estimate. The standard approach is least squares regression, where the estimates are chosen to minimize
. This requires a data‐based rule, or criterion, that will give a reasonable estimate. The standard approach is least squares regression, where the estimates are chosen to minimize