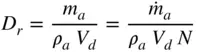There are three useful mean effective pressure parameters – imep, bmep, and fmep. The indicated mean effective pressure (imep) is the net work per unit displacement volume done by the gas during compression and expansion. The name originates from the use of an 'indicator' card used in the past to plot measured pressure versus volume. The pressure in the cylinder initially increases during the expansion stroke due to the heat addition from the fuel, and then decreases due to the increase in cylinder volume.
The brake mean effective pressure (bmep) is the external shaft work per unit volume done by the engine. The name originates from the brake dynamometer used to measure the torque produced by the rotating shaft. Typical values of bmep for vehicular engines depend on the load. A low‐load bmep is about 5 bar, a mid‐load bmep is about 10 bar, and a high‐load bmep is about 20 bar. Use of turbo‐ or supercharging is generally required to produce a high‐load bmep.
Based on torque, the bmep is
(1.15) 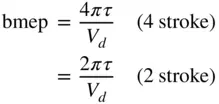
and in terms of power, the bmep is
(1.16) 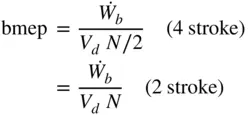
The bmep can also be expressed in terms of piston area 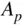 , mean piston speed
, mean piston speed 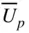 , and number of cylinders
, and number of cylinders 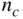 :
:
(1.17) 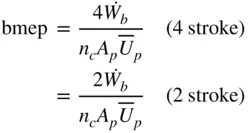
The friction mean effective pressure (fmep) includes the mechanical engine friction, the pumping losses during the intake and exhaust strokes, and the work to run auxiliary components such as oil and water pumps. Accordingly, the friction mean effective pressure (fmep) is the difference between the imep and the bmep. Determination of the fmep is discussed further in Chapter 10.
(1.18) 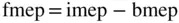
The bmep of two different displacement naturally aspirated automobile engines at wide‐open throttle (WOT) is compared versus mean piston speed in Figure 1.8. Notice that when performance is scaled to be size independent, there is considerable similarity.
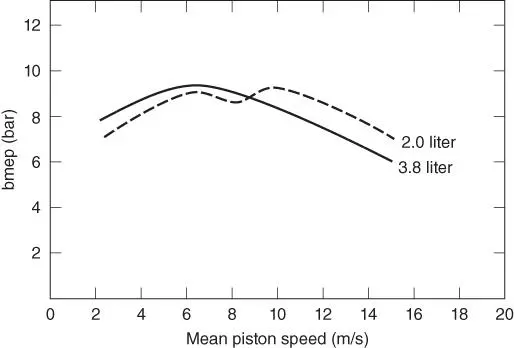
Figure 1.8Brake mean effective pressure at WOT versus mean piston speed for two automotive engines.
A performance parameter of importance for four‐stroke engines is the volumetric efficiency, 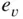 . It is defined as the mass of air
. It is defined as the mass of air  inducted into the cylinder at bottom dead center divided by the mass that would occupy the cylinder volume
inducted into the cylinder at bottom dead center divided by the mass that would occupy the cylinder volume 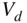 at a density
at a density 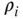 of the intake manifold air. The flow restrictions in the intake system, including the throttle, intake port, and valve, create a pressure drop in the inlet flow, which reduces the density and thus the mass of the gas in the cylinder. The volumetric efficiency is thus a mass ratio and not a volume ratio.
of the intake manifold air. The flow restrictions in the intake system, including the throttle, intake port, and valve, create a pressure drop in the inlet flow, which reduces the density and thus the mass of the gas in the cylinder. The volumetric efficiency is thus a mass ratio and not a volume ratio.
The volumetric efficiency for an engine operating at a speed 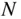 is
is
(1.19) 
The factor of 2 in Equation ( 1.19) accounts for the two revolutions per cycle in a four‐stroke engine. The ideal gas equation is used to determine the air density in the intake manifold,
(1.20) 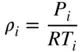
The parameter 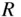 is the ideal gas constant for air with a value of
is the ideal gas constant for air with a value of 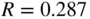 kJ/kg‐K. The intake manifold air density is used as a reference condition instead of the standard atmosphere, so that the effect of a supercharger is not included in the definition of volumetric efficiency. The standard atmosphere is assumed to have a temperature
kJ/kg‐K. The intake manifold air density is used as a reference condition instead of the standard atmosphere, so that the effect of a supercharger is not included in the definition of volumetric efficiency. The standard atmosphere is assumed to have a temperature 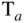 = 298 K and pressure
= 298 K and pressure 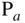 = 101.3 kPa, with a corresponding density
= 101.3 kPa, with a corresponding density  = 1.184 kg/
= 1.184 kg/ 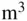 .
.
For two‐stroke cycles, an equivalent volumetric efficiency parameter is the delivery ratio 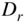 , which is defined in terms of the ambient air density
, which is defined in terms of the ambient air density 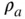 instead of the intake manifold density:
instead of the intake manifold density:
(1.21) 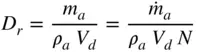
A representative plot of volumetric efficiency versus engine speed of an automotive four‐stroke engine is shown in Figure 1.9. The shape and location of the peaks of the volumetric efficiency curve are very sensitive to the engine speed as well as the manifold configuration. Some configurations produce a flat curve, others produce a very peaked and asymmetric curve. As we will see later, the volumetric efficiency is also influenced by the valve size, valve lift, and valve timing. It is desirable to maximize the volumetric efficiency of an engine since the amount of fuel that can be burned and power produced for a given engine displacement (hence size and weight) is maximized. Although it does not influence in any way the thermal efficiency of the engine, the volumetric efficiency will influence the overall thermal efficiency of the system in which it is installed. As Example 1.1 below indicates, the volumetric efficiency is useful for determination of the air flowrate of an engine of a given displacement and speed.
Читать дальше

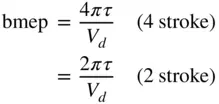
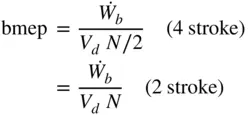
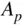 , mean piston speed
, mean piston speed 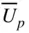 , and number of cylinders
, and number of cylinders 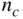 :
: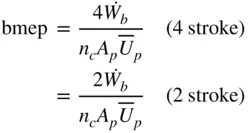
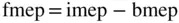

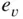 . It is defined as the mass of air
. It is defined as the mass of air  inducted into the cylinder at bottom dead center divided by the mass that would occupy the cylinder volume
inducted into the cylinder at bottom dead center divided by the mass that would occupy the cylinder volume 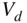 at a density
at a density 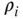 of the intake manifold air. The flow restrictions in the intake system, including the throttle, intake port, and valve, create a pressure drop in the inlet flow, which reduces the density and thus the mass of the gas in the cylinder. The volumetric efficiency is thus a mass ratio and not a volume ratio.
of the intake manifold air. The flow restrictions in the intake system, including the throttle, intake port, and valve, create a pressure drop in the inlet flow, which reduces the density and thus the mass of the gas in the cylinder. The volumetric efficiency is thus a mass ratio and not a volume ratio.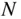 is
is
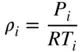
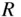 is the ideal gas constant for air with a value of
is the ideal gas constant for air with a value of 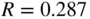 kJ/kg‐K. The intake manifold air density is used as a reference condition instead of the standard atmosphere, so that the effect of a supercharger is not included in the definition of volumetric efficiency. The standard atmosphere is assumed to have a temperature
kJ/kg‐K. The intake manifold air density is used as a reference condition instead of the standard atmosphere, so that the effect of a supercharger is not included in the definition of volumetric efficiency. The standard atmosphere is assumed to have a temperature 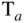 = 298 K and pressure
= 298 K and pressure 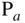 = 101.3 kPa, with a corresponding density
= 101.3 kPa, with a corresponding density  = 1.184 kg/
= 1.184 kg/ 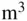 .
.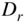 , which is defined in terms of the ambient air density
, which is defined in terms of the ambient air density 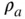 instead of the intake manifold density:
instead of the intake manifold density: