(2.2) 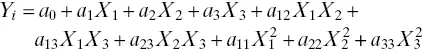
The estimated model equations (both coded and actual), regression coefficients, R 2, adjusted R 2, regression ( P ‐value and F ‐value), and standard deviation related to the effect of the three CPPs (independent variables) are presented in Table 2.8. Although the actual model equation contains the levels specified in the original units for each CPP, this equation should not be used to determine the relative impact of each CPP (factor). Therefore, the coded model equation is used for identifying the relative impact of the CPPs by comparing the regression coefficient values of each factor. Nevertheless, a positive value in the regression equation represents an effect that favors optimization due to synergistic effect, while a negative value indicates an inverse relationship or antagonistic effect between the factor and the responses (Woitiski et al. 2009). It should be mentioned that nonsignificant ( p < 0.005) linear terms (main CCD effect) were included in the final reduced model if quadratic or interaction terms containing these variables were found to be significant ( p < 0.05). In the present study, the response surface analysis demonstrated that the second‐order polynomial used for MPS has a higher coefficient of determination ( R 2= 0.8186) compared to ZP value ( R 2= 0.6525) and PDI value ( R 2= 0.7188). The obtained coefficient of determination showed that >82% of the response variation of the MPS, PDI, and ZP values could be described by response surface models as the function of the CPPs. It was observed that the lack of fit had no indication of significant ( p < 0.05) for the final reduced model, therefore providing the satisfactory fitness of the RSM to the significant independent variables (factors) effect. From Table 2.8, it was observed that two independent variables ( A and B ) exhibited a positive effect on the response of ZP ( R 3). Both MPS ( R 1) and PDI ( R 2) showed a positive effect for all of the tested three independent variables ( A , B , and C ). The interaction coefficients with more than one factor, or higher order terms in the regression equation, represent the interaction between terms or the quadratic relationship, respectively, which suggest a nonlinear relationship between factors and responses (Motwani et al. 2008). Therefore, a different degree of response than it is originally predicted by regression equation may be expected from the independent variables as they are varied at different levels or more than one factor or variables is changed simultaneously (Woitiski et al. 2009). In the present face‐centered CCD modeling, all the responses (MPS, PDI, and ZP or R 1, R 2, and R 3) were affected by the interaction of independent variables and hence displaying a quadratic relationship. The interaction effects between B and C was favorable for response R 3(showing a positive regression coefficient value of 2.06) and non‐favorable for R 1and R 2(showing negative regression coefficient values). The interaction effects between A and B was favorable for response R 1(showing a positive regression coefficient value of 13.75) and non‐favorable for R 2and R 3(showing negative regression coefficient values). However, it was observed that the interaction between A and C had an inverse effect for all three responses variables studied. Noticeably, quadratic effects ( A 2, B 2, and C 2) were also seen between all three independent variables and all of the studied three response variables (MPS, PDI, and ZP or R 1, R 2, and R 3). The highest and positive quadratic effect for all three independent variables was noticed for the MPS response variable R 1(showing a positive regression coefficient value of 15.35). Similarly, the highest and negative quadratic effect was also noted for the MPS response variable R 1(showing a negative regression coefficient −118.30).
TABLE 2.8. Estimated Coded and Actual Model Equations Along with ANOVA of Regression Coefficients for Face‐Centered Central Composite Design (CCD) Effects (Main or Linear, Quadratic and Interaction) Against the Critical Quality Attributes (CQAs, Dependent Variables) to Determine the Best Fitted Quadratic Equation
| CQAs |
Model Equations |
R 2 |
Adjusted R 2 |
| Mean particle size ( R 1) |
Coded: R 1 =569.86 + 65.20 × A + 25.21 × B + 43.03 × C + 13.75 × AB − 55.18 × AC − 10.38 × BC + 15.35 × A 2− 118.30 × B 2− 91.00 × C 2 |
0.8186 |
0.6553 |
| Actual:PS = −5992.56500 + 663.59545 × a + 88.29447 × b + 120.25931 × c + 4.58333 × a × b − 8.82800 × a × c − 0.138333 × b × c + 61.41818 × a 2− 3.28598 × b 2− 0.582371 × c 2 |
| Polydispersity index ( R 2) |
Coded: R 2= 0.6038 + 0.0325 × A + 0.0234 × B + 0.0960 × C − 0.0106 × AB − 0.0649 × AC − 0.0494 × BC + 0.0180 × A 2+ 0.0075 × B 2+ 0.1455 × C 2 |
0.7188 |
0.4658 |
| Actual:PDI = −9.27017 + 0.800295 × a + 0.061847 × b +0.194161 × c −0.003542 × a × b − 0.010380 × a × c − 0.000658 × b × c + 0.071818 × a 2+ 0.000207 × b 2− 0.000931 × c 2 |
| Zeta potential ( R 3) |
Coded: R 3= 28.89 + 0.0500 × A + 1.32 × B − 2.76 × C − 2.21 × AB − 0.9125 × AC + 2.06 × BC − 0.8136 × A 2− 1.56 × B 2− 4.26 × C 2 |
0.6525 |
0.3397 |
| Actual:ZP =−180.64250 + 31.48864 × a − 0.037576 × b + 4.44347 × c − 0.737500 × a × b − 0.146000 × a × c + 0.027500 × b × c − 3.25455 × a 2− 0.043434 × b 2− 0.027287 × c 2 |
| CCD effects |
Variables |
R 1 |
R 2 |
R 3 |
| F‐value |
P‐value |
F‐value |
P‐value |
F‐value |
P‐value |
| Linear term |
A |
7.61 |
0.0202 |
1.09 |
0.3219 |
0.0013 |
0.9714 |
| B |
1.14 |
0.3111 |
0.5629 |
0.4704 |
0.9391 |
0.3554 |
| C |
3.32 |
0.0986 |
9.47 |
0.0117 |
4.11 |
0.0702 |
| Interaction term |
AB |
0.2709 |
0.6141 |
0.0928 |
0.7668 |
2.11 |
0.1769 |
| AC |
4.36 |
0.0633 |
3.46 |
0.0924 |
0.3590 |
0.5624 |
| BC |
0.1542 |
0.7028 |
2.01 |
0.1872 |
1.83 |
0.2054 |
| Quadratic term |
A 2 |
0.1161 |
0.7403 |
0.0911 |
0.7689 |
0.0981 |
0.7605 |
| B 2 |
6.89 |
0.0254 |
0.0157 |
0.9027 |
0.3624 |
0.5606 |
| C 2 |
4.08 |
0.0711 |
5.99 |
0.0344 |
2.69 |
0.1317 |
Note: A/a : Castor oil, B/b : Chitosan, C/c : Poloxamer.
Читать дальше