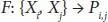Table 2.1summarizes the techniques used in the related studies for One- shot learning. Accordingly, most studies have used capsule-based techniques in recent years. This could be because capsule networks show better generalization with small datasets.
In this chapter, we design a Siamese network similar to Koch et al. but with useful modifications to accommodate more complex details grabbed by capsules. Siamese network is a twin network, which takes two images as input and feeds to the weight sharing twin network. Our contributions in this chapter include exploring the applicability of capsules in Siamese networks, introducing novel architecture to handle intricate details of capsule output, and integrating recent advancement to go deep with capsule networks [33, 34] into Siamese networks.
Table 2.1 Comparison of related studies.
| Related work |
Bayesian network |
Neural network |
Siamese neural network |
Capsule network |
| Lake et al. [6] |
X |
|
|
|
| Koch et al. [7] |
X |
|
X |
|
| Hinton et al. [11] |
|
|
|
X |
| Bertinetto et al. [24] |
|
X |
|
|
| Chen et al. [13] |
|
X |
|
|
| Fei-Fei et al. [4] |
X |
|
|
|
| Lie et al. [15] |
|
X |
|
|
| Bromley et al. [28] |
|
|
X |
|
| Kumar et al. [31] |
|
|
|
X |
| Zhao et al. [32] |
|
|
|
X |
| Sabour et al. [9] |
|
|
|
X |
| Sethy et al. [12] |
|
X |
|
|
In this research, we define character image classification as a subproblem of character verification and develop an image verification model which learns a function F, as shown in Equation (2.1)
(2.1) 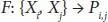
which gives the Pi,j probability of two images, Xi and Xj belonging to the same category. We expect the model to learn a general representation of images that could be applied to unseen data without any further training. After fine-tuning the model for the verification task, we use a one-shot learning approach to classify images, as explained in Section 2.3.1.
We propose a Siamese architecture comprising of a twin capsule network and a fully connected network, for character verification. This architecture mainly consists of a weight sharing twin network, vector difference layer and a fully connected network, as shown in Figure 2.1. Siamese network takes two input images, run them through a feature extraction process, comparison layers, and finally gives out the probability of belonging to the same category. Twin network starts with a convolutional layer and has four capsule layers before the fully connected entity capsule layer. Results from twin network merged using a vector difference function and input to the fully connected part to predict the final probability. We decompose the Siamese network to three main sections: Twin network, Difference layer and Fully connected network, to explain the structure and functionality.
Twin network: Twin network consists of two similar networks that share weights between them. The purpose of sharing weights is getting the same output from both networks if the same image feed to them. Since we wanted the twin network to learn how to extract features that could help distinguish images; convolutional layers, capsule layers and deep capsule layers were used and deep capsule layers-based model gave the best performance.
The capsule network consists of four layers. Since we consider relatively simpler images with plain backgrounds, having many layers has a less effect. The first layer is a convolutional layer with 256, 9 × 9 kernels with a stride 5 to discover basic features in the 2D image. Second, third, and fourth layers are capsule layers with 32 channels of 4-dimensional capsules, where each capsule consists of 4 convolutional units with a 3 × 3 kernel and strides of 2 and 1, respectively. Next capsule layer contains 16 channels of 6-dimensional capsules. Each of them consists of a convolutional unit with a 3 × 3 kernel and stride of 2. The sixth layer is a fully connected capsule layer named as entity capsule layer. It contains 20 capsules of 16-dimension. We use dynamic routing proposed by Ref. [9], between final convolutional capsule layer and entity capsule layer with three routing iterations.
Vector difference layer: After twin network identifies and extracts important features in two input images, the vector difference layer is used to compare those features to get a final decision about similarity. Each capsule in the twin network is trained to extract an exact type of property or entity such as an object or part of an object. Here, the length and the direction of the output vector is determined by the probability of feature detection and the state of the detected feature, respectively [11]. For example, when an identified feature is changed its state by a move, the probability remains the same with the vector length, while orientation changes. Due to this property, it is not enough to take scalar difference using L1 distance but needs to use more complex vector difference and analyse it. We obtain 20 vectors of dimension 16 after the difference layer and feed it to a fully connected network.
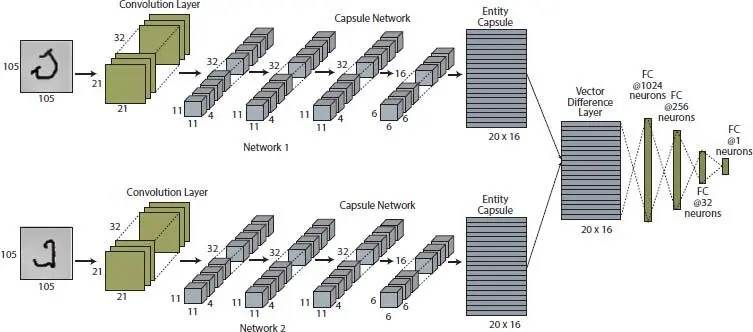
Figure 2.1 Siamese network architecture.
Fully connected network: Fully connected network comprises four fully connected layers with parameters as shown by Figure 2.1. Except for the last fully connected layer which has sigmoid activation, other fully connected layers use Rectified Linear Unit (ReLU) activation [35]. In this study, multiple fully connected layers are used to analyse the complex output of the vector difference layer to get an accurate probability.
2.3.1 One-Shot Learning Implementation
The goal of this study is classifying characters in new alphabets. After fine-tuning the model for the verification job, we expect that it has learned a general enough function to distinguish between any two images. Hence, we could model character classification as a one-shot learning task that uses only one sample to learn or perform a particular task [6]. This study creates a reference set for all the possible classifications with only one image and then feed the verification model with the pairs created by using test image and one image from the reference set and predict a class using the similarity score given by the model. This approach is further extended to improve accuracy and testing purposes, as explained in Section 2.4.
2.3.2 Optimization and Learning
The proposed methodology learns the optimal model parameters by optimizing a cost function, which is defined over the expected output and the actual result. Moreover, binary cross-entropy function [36], is used as given in Equation (2.2), to quantify the prediction accuracy. Here θ denotes the parameters of the model. The symbols xi, xj. and yi,j represent the input image, reference image and the expected output, respectively. The output of the function F increases if the reference and the test images are equal. Otherwise, the function tries to decrease the value. The Adam optimizer [37], is used to optimize this cost function.
Читать дальше