3 λ = 0.001 m
Como se puede ver en el resultado, la longitud de onda de la radiación está muy por encima de la visible por el ojo humano.
Para conocer la cantidad de energía solar que llega a la frontera exterior que delimita la atmósfera, se establece la denominada constante solar,la cual mide la radiación sobre una superficie orientada en la dirección de los rayos solares. Su valor es de 1353 W/m 2y varía en torno a un 3 %, debido a la órbita elíptica de la tierra.
3.4. Radiación solar en la superficie de la tierra
La energía que se recibe del sol se compone de radiación electromagnética, pero no toda se produce en forma de luz visible. También se recibe radiación ultravioleta e infrarroja, que son invisibles para el ojo humano y cuya presencia no se puede ignorar.

Sabía que...
El fenómeno del bronceado de la piel se debe a la presencia de la radiación ultravioleta, invisible para el ojo humano.
Existen algunos factores fundamentales que determinan el nivel de la radiación recibida en la superficie terrestre. Estos son:
1 Condiciones atmosféricas y ambientales del lugar.
2 Situación geográfica.
3 Movimiento de la tierra.
3.5. Radiación solar y métodos de cálculo
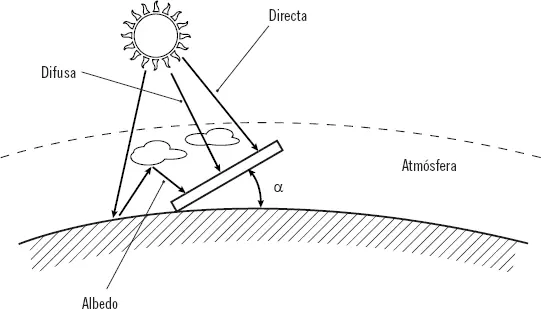
Antes de llegar a la superficie de la tierra, la radiación es reflejada al entrar en la atmósfera por la presencia de las nubes, el vapor de agua, etc., y dispersada por las moléculas de agua, el polvo en suspensión... Debido a esto, la radiación solar que llega a la superficie terrestre procede de tres componentes:
1 Radiación directa (B): formada por los rayos que provienen directamente del sol, es decir, que no llegan a ser dispersados.
2 Radiación difusa (D): porocede de toda la bóveda celeste, excepto la que llega del sol, y está originada por los efectos de dispersión mencionados anteriormente.
3 Radiación del albedo (R): procedente del suelo, se debe a la reflexión de parte de la radiación incidente sobre montañas, lagos, edificios, etc. Depende muy directamente de la naturaleza de estos elementos.
La suma de estos tres componentes da lugar a la radiación global (G),que se determina: G = B + D + R.
3.6. Energía incidente sobre una superficie plana inclinada
En el caso de tener un plano orientado al ecuador con una inclinación ß sobre el plano horizontal del lugar, se puede calcular el ángulo de incidencia de la radiación solar directa con dicho plano, mediante la expresión:
cos θ = cos (L - ß) · cos δ · cos ω + sin (L - ß) sin δ
Siendo:
1 θ = Ángulo de incidencia formado por la normal a la superficie y el rayo incidencia de ella.
2 L = Latitud del punto de la superficie terrestre considerado, el cual es el ángulo que forma el radio terrestre que pasa por dicho punto con el ecuador.
3 ß = Ángulo de inclinación.
4 ω = Ángulo horario.
5 δ = Declinación.
La radiación total sobre una superficie inclinada a partir de la radiación horizontal, considerando periodos relativamente cortos (una hora), se obtiene de:
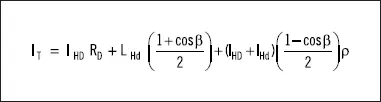
Siendo:
1 It = Radiación total sobre una superficie inclinada. IHD = Componente directa de la radiación sobre el plano horizontal. IHd = Componente difusa de la radiación solar sobre el plano horizontal. RD = Relación entre la componente directa de la radiación solar sobre una superficie inclinada y la radiación directa sobre una superficie horizontal. ρ = Reflexividad del suelo.
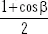 Mide la proporción de bóveda celeste vista por la superficie inclinada, respecto a la que ve un plano horizontal.
Mide la proporción de bóveda celeste vista por la superficie inclinada, respecto a la que ve un plano horizontal.
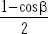 Mide la proporción de suelo que ve la superficie inclinada.
Mide la proporción de suelo que ve la superficie inclinada.
En los cálculos de las aportaciones solares recibidas por la superficie captadora, se hace necesario conocer la relación (R) entre la radiación media diaria mensual (H βmedia) recibida por la superficie captadora y la radiación media diaria mensual (H) recibida por una superficie horizontal. Es decir:
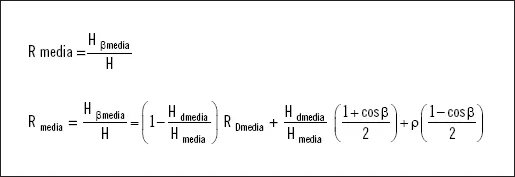
Donde:
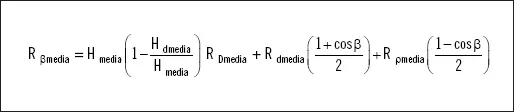
3.7. Orientación e inclinación óptima anual, estacional y diaria
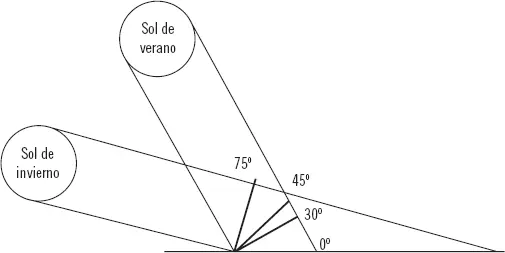
A la hora de aprovechar al máximo la energía solar, es necesario tener en cuenta que el sol no se encuentra a la misma altura (respecto al horizonte) en invierno que en verano, lo que significa que la inclinación de los paneles fotovoltaicos no puede ser fija si se quiere que, en todo momento, esos paneles se encuentren perpendicularmente orientados al sol.
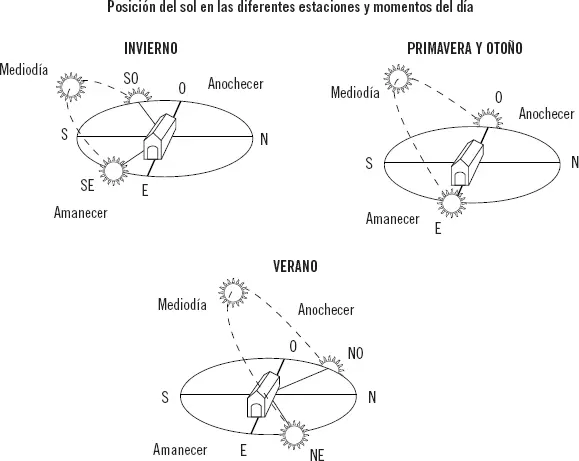
La inclinación óptima de cualquier captador solar se establece en función de la latitud y la aplicación:
1 Para la utilización en invierno: 10ª mayor que la latitud.
2 Para la utilización en primavera y verano: 20ª menor que la altitud.
3 Paralautilizaciónuniformedurantetodoelaño:10ªmayorquelalatitud.

Definición
Latitud
La latitud mide el ángulo desde un punto cualquiera del planeta con respecto al ecuador. Este ángulo se mide desde el meridiano (línea imaginaria que rodea la tierra y que pasa por los polos) del lugar correspondiente.
En las latitudes españolas (40º aproximadamente), la orientación óptima de los módulos fotovoltaicos es hacia el sur. Sin embargo, la energía que se deja de generar por estar estos módulos orientados hacia el sureste o suroeste, representa solo un 0,2 % por cada grado de desviación respecto al sur.
Del mismo modo, la inclinación óptima de los módulos fotovoltaicos depende de la latitud del lugar donde se instalen, lo que implica una inclinación entre 5º y 10º respecto a la latitud (por ejemplo, resultarían unos 35º en el centro de la península), y de la época del año en la que se quiera maximizar la producción.
En cualquier caso, es recomendable una inclinación superior a los 15º, para permitir que el agua de la lluvia se escurra. Donde nieva con cierta frecuencia, es recomendable una inclinación a partir de los 45º, para favorecer el deslizamiento de la nieve. En definitiva, es recomendable acercarse a las condiciones óptimas de la instalación: orientación sur e inclinación entre 5º y 10º menos que la latitud.
Las denominadas horas de pico solarconstituyen un parámetro fundamental para el dimensionado de los sistemas fotovoltaicos. Corresponden al número de horas en las que cada metro cuadrado de superficie captadora obtiene, de modo constante, 1000 W de energía. El número de horas pico de un día concreto, se puede calcular dividiendo la energía producida en ese día entre 1000 W/m 2. En España, la media de horas solares pico es de tres a seis, aunque varía entre el norte y el sur, y de invierno a verano.
Читать дальше



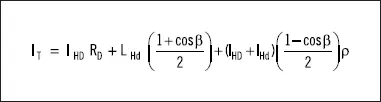
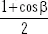 Mide la proporción de bóveda celeste vista por la superficie inclinada, respecto a la que ve un plano horizontal.
Mide la proporción de bóveda celeste vista por la superficie inclinada, respecto a la que ve un plano horizontal.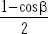 Mide la proporción de suelo que ve la superficie inclinada.
Mide la proporción de suelo que ve la superficie inclinada.















