Resonances occur where m (Ω − Ω p ) = n κ, where Ω is the circular angular velocity, Ω p is the pattern speed (uniform angular rotation rate of the spiral pattern), κ is the radial (epicyclic) frequency, and m/n is the number of radial oscillations per single orbit in the reference frame rotating at Ω p . Both Ω and κ are functions of galactocentric radius. The main ring-forming resonances are the outer and inner Lindblad resonances (OLR and ILR, respectively), for which m = 2 n =±1, and the outer and inner 4:1 resonances (O4R and I4R, respectively), for which m = 4 and n =±1. In any normal galaxy, there will likely be two ILRs, with the innermost one called the inner ILR (or IILR) and the outermost one called the outer ILR (or OILR). Another important (but not necessarily ring-forming) resonance is the corotation resonance (CR), where Ω p = Ω. The locations of all of these resonances can be determined by plotting the curves Ω and Ω ± κ/m versus galactocentric radius and reading the radii where these functions equal Ω p .
Support for the resonance idea comes principally from (a) the morphology of galactic rings (Buta and Crocker 1991; Buta 1995b); (2) statistical studies of intrinsic shapes and orientations of galactic rings with respect to bars (Buta 1995b; Comerón et al . 2014); and (3) detailed studies and numerical modeling of individual cases such as NGC 3081 (Buta and Purcell 1998) and NGC 6782 (Lin et al . 2008). Rings are relatively narrow features, most frequently associated with gas. In particular, nuclear rings are often conspicuous sites of star formation. In general, rings form when gas is accumulating in the bar resonance locations, since the gravity torques from the bar are then canceling out. The angular momentum transport is discussed in detail in Buta and Combes (1996).
Figure 1.28shows three galaxies from the Catalogue of Southern Ringed Galaxies (Buta 1995b) having well-defined outer resonant features. The white circles in the images show the estimated location of the CR in each galaxy based on the “gap method”, a way of determining the radius of the CR using dark gaps lying along the line perpendicular to the bar axis (Buta 2017b). By using this method, and assuming the rotation curves for the galaxies are approximately flat, the schematics show the locations of the other major resonances, I4R, O4R and OLR. The results from these galaxies and 47 others examined by Buta (2017b) provide a consistent picture of systems where 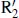 rings lie slightly outside the OLR, R 1and
rings lie slightly outside the OLR, R 1and 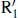 rings lie near but inside the OLR, and inner rings and bars lie close to the I4R. The ILR was once thought to play a major role in nuclear ring formation, but this view was challenged by Regan and Teuben (2004), who argued that the most reliable interpretation of these features is in terms of an orbit transition region inside the bar.
rings lie near but inside the OLR, and inner rings and bars lie close to the I4R. The ILR was once thought to play a major role in nuclear ring formation, but this view was challenged by Regan and Teuben (2004), who argued that the most reliable interpretation of these features is in terms of an orbit transition region inside the bar.
Ringed galaxies and invariant manifolds : Romero-Gomez et al . (2006) proposed an alternative to the resonance interpretation of galactic rings. In this idea, the R 1, 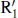 ,
, 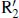 and
and 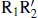 subclasses of outer rings and pseudorings in barred galaxies can all be interpreted in terms of invariant manifolds that emanate from the unstable L 1and L 2Lagrangian points near the ends of a bar. In this interpretation, rings are not necessarily resonant features, but are features mapped by the manifolds as tube-guided homoclinic, heteroclinic and escaping chaotic orbits. In homoclinic orbits, a spiral emanates from L 1or L 2and closes at L 2or L 1, respectively, after winding 180°; this is a morphology consistent with R 1and
subclasses of outer rings and pseudorings in barred galaxies can all be interpreted in terms of invariant manifolds that emanate from the unstable L 1and L 2Lagrangian points near the ends of a bar. In this interpretation, rings are not necessarily resonant features, but are features mapped by the manifolds as tube-guided homoclinic, heteroclinic and escaping chaotic orbits. In homoclinic orbits, a spiral emanates from L 1or L 2and closes at L 2or L 1, respectively, after winding 180°; this is a morphology consistent with R 1and 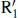 rings. In heteroclinic orbits, a spiral emanates from L 1or L 2and closes at L 1or L 2, respectively, after winding 360°; this is a morphology consistent with the double outer ring/pseudoring morphology
rings. In heteroclinic orbits, a spiral emanates from L 1or L 2and closes at L 1or L 2, respectively, after winding 360°; this is a morphology consistent with the double outer ring/pseudoring morphology 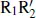 . Finally, in an escaping orbit, a spiral emanates from L 1or L 2and winds outward, never to intersect the opposing Lagrangian point; these can account for the morphology of
. Finally, in an escaping orbit, a spiral emanates from L 1or L 2and winds outward, never to intersect the opposing Lagrangian point; these can account for the morphology of 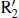 outer pseudorings.
outer pseudorings.

Figure 1.28. Three galaxies showing outer resonant subclass features. The white circle in each image is the estimated location of the corotation resonance (CR) based on the gap method of Buta (2017b). The schematics show the locations of other resonances relative to visually mapped ring and pseudoring features, assuming a flat rotation curve. The method assumes that light deficits on the line perpendicular to the bar axis trace the location of unstable Lagrangian points L 4 and L 5 (indicated as L4 and L5 each plot). These points are assumed to trace the location of the CR. The other resonances highlighted are the inner 4:1 resonance (I4R), the outer 4:1 resonance (O4R) and the outer Lindblad resonance (OLR)
The potential-density phase shift and galactic secular evolution : Models of barred galaxies like those of Schwarz (1981, 1984) and Rautiainen and Salo (2000) suggest that rings are products of the evolution of spiral patterns near resonances. That is, a ring begins as a pseudoring and then evolves into a more closed feature. However, very few galaxies show the influence of resonances as strongly as do cases like NGC 3081 or any galaxy showing outer resonant subclass features. This is because the typical inner variety for spirals is (s), the typical nuclear variety is no nuclear feature and the typical outer variety is no outer feature. The question to ask, then, is not why some galaxies have rings, but why so many do not.
The theoretical work of Zhang (2018 and references therein) challenges previous views on galaxy dynamics and provides a real mechanism for the secular evolution of the stellar distribution of a spiral galaxy, not just the interstellar gas distribution. The galaxy-disk mass distribution, contributed mostly by stellar mass, is part of the so-called “basic state” used to calculate spiral density wave perturbations. In addition to the axisymmetric (i.e. azimuthally averaged) mass distribution, determined observationally from disk surface brightness and color, the basic state specification includes also the axisymmetric rotation speed (with contributions from the halo and bulge, in addition to the contribution from the disk) and velocity dispersion, with all three usually specified as a function of galactocentric radius. The key factor for the evolution of the basic-state mass distribution is an azimuthal phase shift (phase offset in angles) between a self-consistent spiral perturbation potential, and the density this potential gives rise to. The spiral can arise as a mode in an initially featureless disk, and if it can achieve a quasi-steady state, angular momentum can be taken away from the inner disk, transferred outward and deposited onto the outer disk, leading to the slow buildup of a central mass concentration and an extended outer disk.
Читать дальше

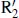 rings lie slightly outside the OLR, R 1and
rings lie slightly outside the OLR, R 1and 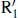 rings lie near but inside the OLR, and inner rings and bars lie close to the I4R. The ILR was once thought to play a major role in nuclear ring formation, but this view was challenged by Regan and Teuben (2004), who argued that the most reliable interpretation of these features is in terms of an orbit transition region inside the bar.
rings lie near but inside the OLR, and inner rings and bars lie close to the I4R. The ILR was once thought to play a major role in nuclear ring formation, but this view was challenged by Regan and Teuben (2004), who argued that the most reliable interpretation of these features is in terms of an orbit transition region inside the bar.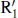 ,
, 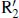 and
and 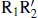 subclasses of outer rings and pseudorings in barred galaxies can all be interpreted in terms of invariant manifolds that emanate from the unstable L 1and L 2Lagrangian points near the ends of a bar. In this interpretation, rings are not necessarily resonant features, but are features mapped by the manifolds as tube-guided homoclinic, heteroclinic and escaping chaotic orbits. In homoclinic orbits, a spiral emanates from L 1or L 2and closes at L 2or L 1, respectively, after winding 180°; this is a morphology consistent with R 1and
subclasses of outer rings and pseudorings in barred galaxies can all be interpreted in terms of invariant manifolds that emanate from the unstable L 1and L 2Lagrangian points near the ends of a bar. In this interpretation, rings are not necessarily resonant features, but are features mapped by the manifolds as tube-guided homoclinic, heteroclinic and escaping chaotic orbits. In homoclinic orbits, a spiral emanates from L 1or L 2and closes at L 2or L 1, respectively, after winding 180°; this is a morphology consistent with R 1and 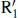 rings. In heteroclinic orbits, a spiral emanates from L 1or L 2and closes at L 1or L 2, respectively, after winding 360°; this is a morphology consistent with the double outer ring/pseudoring morphology
rings. In heteroclinic orbits, a spiral emanates from L 1or L 2and closes at L 1or L 2, respectively, after winding 360°; this is a morphology consistent with the double outer ring/pseudoring morphology 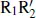 . Finally, in an escaping orbit, a spiral emanates from L 1or L 2and winds outward, never to intersect the opposing Lagrangian point; these can account for the morphology of
. Finally, in an escaping orbit, a spiral emanates from L 1or L 2and winds outward, never to intersect the opposing Lagrangian point; these can account for the morphology of 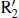 outer pseudorings.
outer pseudorings.











