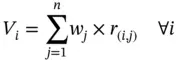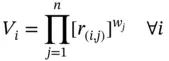Omid Bozorg-Haddad - A Handbook on Multi-Attribute Decision-Making Methods

At this junction, the decision‐maker creates a commensurable decision‐matrix by normalizing the elements of the matrix, using ( Eqs. 2.4– 2.7). This step is vital to compose a logical and viable decision‐making process, for otherwise, combining the nonnormalized values to obtain the overall scores of the alternatives would yield meaningless elements.

The following equation is employed to aggregate the normalized preference values of alternatives (Churchman and Ackoff 1954):

(2.9)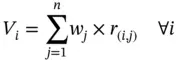

in which V i= the overall preference of the i th alternative. Equation (2.9)is found on most compensatory methods and implies that poor performance of an alternative with respect to some criteria can be compensated for by high performance by other criteria.

Despite its simplicity, the WSM remains a top choice of decision‐makers for evaluating an MADM problem. A conceptually similar method to WSM is the weighted product method (WPM), which is discussed in Section 2.3.

The WPM employs multiplication for synthesizing the attributes' performance values, each of which is raised to the power of the corresponding attributes' weights. In essence, compared to the WSM, the WPM penalizes alternatives with poor attribute preference values more heavily (Triantaphyllou and Mann 1989; Chang and Yeh 2001; San Cristóbal 2012). WPM has been successfully implemented in bidding strategies (Wang et al. 2010), business strategic planning (Chang and Yeh 2001), energy resources management (Pohekar and Ramachandran 2004), environmental evaluations (Zhou et al. 2006), technological instrument selection (Savitha and Chandrasekar 2011), supply chain management (Chou et al. 2008), and waste management (Cheng et al. 2003).

The WPM follows the same basic steps applied in the WSM. The following is a stepwise procedure to implement the WPM in an MADM problem:

Step 1: Defining the decision‐making problem

Step 2: Normalizing the elements of the decision‐matrix

Step 3: Aggregating the preference of alternatives

Equation (2.10)synthesizes the alternatives' performance values (Chang and Yeh 2001):

(2.10)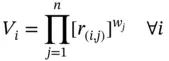

This method is also considered as a compensatory MADM method where the assumption of criteria independency is made (Saaty and Ergu 2015).

MADM problems have extensive theoretical and practical foundations. Concerning MADM it has been demonstrated how to mathematically express decision‐making problem through an instrument called the decision‐matrix. A decision‐matrix is, generally, composed of four features, namely, alternatives, criteria, the weights of criteria, and the performance value of alternatives. Additionally, the importance of normalizing the element of the decision‐matrix, which is a mathematical procedure through which the preference values of the decision‐matrix are rendered dimensionless, was also reviewed in this chapter. Lastly, two of the majorly implemented, basic MADM methods, namely, WSM and WPM, were presented, and stepwise instructions for each method were listed. The WSM and WPM are compensatory methods founded on the assumption of criteria independence. Tough and more advanced methods are available, the WSM and WPM remain relevant. They constitute the foundation on which most state‐of‐the‐arts MADM methods are founded upon.

1 Andrews, S.S. and Carroll, C.R. (2001). Designing a soil quality assessment tool for sustainable agroecosystem management. Ecological Applications 11 (6): 1573–1585.

2 Athawale, V.M. and Chakraborty, S. (2011). A comparative study on the ranking performance of some multi‐criteria decision‐making methods for industrial robot selection. International Journal of Industrial Engineering Computations 2 (4): 831–850.

3 Chang, Y.H. and Yeh, C.H. (2001). Evaluating airline competitiveness using multiattribute decision making. Omega 29 (5): 405–415.

4 Cheng, S., Chan, C.W., and Huang, G.H. (2003). An integrated multi‐criteria decision analysis and inexact mixed integer linear programming approach for solid waste management. Engineering Applications of Artificial Intelligence 16 (5‐6): 543–554.

5 Chou, S.Y., Chang, Y.H., and Shen, C.Y. (2008). A fuzzy simple additive weighting system under group decision‐making for facility location selection with objective/subjective attributes. European Journal of Operational Research 189 (1): 132–145.

6 Churchman, C.W. and Ackoff, R.L. (1954). An approximate measure of value. Journal of the Operations Research Society of America 2 (2): 172–187.

7 Ebert, U. and Welsch, H. (2004). Meaningful environmental indices: A social choice approach. Journal of Environmental Economics and Management 47 (2): 270–283.

8 Goicoechea, A., Stakhiv, E.Z., and Li, F. (1992). Experimental evaluation of multiple criteria decision models for application to water resources planning. Journal of the American Water Resources Association 28 (1): 89–102.

9 Hobbs, B.F., Chankong, V., Hamadeh, W., and Stakhiv, E.Z. (1992). Does choice of multicriteria method matter? An experiment in water resources planning. Water Resources Research 28 (7): 1767–1779.

10 Howard, A.F. (1991). A critical look at multiple criteria decision making techniques with reference to forestry applications. Canadian Journal of Forest Research 21 (11): 1649–1659.

11 Jato‐Espino, D., Castillo‐Lopez, E., Rodriguez‐Hernandez, J., and Canteras‐Jordana, J.C. (2014). A review of application of multi‐criteria decision making methods in construction. Automation in Construction 45: 151–162.

12 Kang, S.M. (2002). A sensitivity analysis of the Korean composite environmental index. Ecological Economics 43 (2): 159–174.

13 Ma, J., Fan, Z.P., and Huang, L.H. (1999). A subjective and objective integrated approach to determine attribute weights. European Journal of Operational Research 112 (2): 397–404.

14 Olson, D.L., Moshkovich, H.M., Schellenberger, R., and Mechitov, A.I. (1995). Consistency and accuracy in decision aids: experiments with four multiattribute systems. Decision Sciences 26 (6): 723–747.

15 Pohekar, S.D. and Ramachandran, M. (2004). Application of multi‐criteria decision making to sustainable energy planning: a review. Renewable and Sustainable Energy Reviews 8 (4): 365–381.

16 Saaty, T.L. and Ergu, D. (2015). When is a decision‐making method trustworthy? Criteria for evaluating multi‐criteria decision‐making methods. International Journal of Information Technology and Decision Making 14 (06): 1171–1187.

17 San Cristóbal, J.R. (2011). Multi‐criteria decision‐making in the selection of a renewable energy project in Spain: the VIKOR method. Renewable Energy 36 (2): 498–502.

18 San Cristóbal, J.R. (2012). Weighted sum method and weighted product method. In: Multi Criteria Analysis in the Renewable Energy Industry (ed. J.R. San Cristobal), 19–22. London, UK: Springer.

19 Savitha, K. and Chandrasekar, C. (2011). Vertical Handover decision schemes using SAW and WPM for network selection in heterogeneous wireless networks. Global Journal of Computer Science and Technology 11 (9): 19–24.