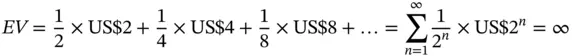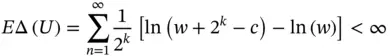To grasp the magnitude of the described conundrum, consider for a moment, the answer of classical mathematics to the described question. The expected value of the prize resulting from playing this game is (Bernoulli 1738):
(1.1) 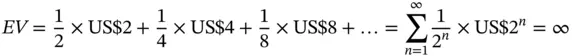
in which EV = the expected value turns out to be infinity. Accordingly, a player would be willing to pay any price to participate in the described game. However, this result defies human behavior since no one would be willing to pay a limitless amount of cash to engage in this game (Rieger and Wang 2006). The answer to the St. Petersburg paradox, which revolutionized the way in which decision‐making problems were analyzed, did not surface itself until Daniel Bernoulli (1700–1782) published his influential research on utility theory in 1738. The concrete discussions describing the solution of the St. Petersburg paradox in detail are skipped here; yet, it is noteworthy that the remarkable solution that enabled Daniel Bernoulli to solve the aforementioned paradox relied on the fact that humans make decisions based not on the expected value, but rather, on the utility value. Specifically, assume that a prospective player has a wealth of w dollars, that the charge for entering the game equals c dollars, and that the player’s utility function is U ( w ) = ln( w ). It can be shown that under these circumstances, the expected incremental (or marginal) utility of playing this game [ E Δ( U )] is finite:
(1.2) 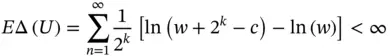
Therefore, a prospective player whose wealth equals US$10 6should be willing to pay up to US$20.88 to play the game; or US$10.95 if the wealth is US$10 3, and so on and so forth, because the amounts the player would be willing to pay maximize his expected incremental utility. The implication of the utility value is that humans choose the alternative with the highest expected utility value when confronting the MADM problems. A chronologic overview of the most fundamental and influential MADM methods, which would be discussed within this book, is presented in Table 1.2.
Table 1.2 A chronologic overview of the most influential MADM methods.
| MADM Methods |
Utility function |
Bernoulli (1738) |
| Weighted sum method (WSM) |
Churchman and Ackoff (1954) |
| ELECTERE I |
Benayoun et al. (1966) |
| ELECTERE II |
Roy and Bertier (1971) |
| Analytic hierarchy process (AHP) |
Saaty (1977) |
| ELECTERE III |
Roy (1978) |
| TOPSIS |
Hwang and Yoon (1981) |
| ELECTERE IV |
Roy and Hugonnard (1982) |
| PROMETHEE I |
Brans (1982) |
| PROMETHEE II |
Vincke and Brans (1985) |
| PROMETHEE III |
Brans et al. (1986) |
| PROMETHEE IV |
Mladineo et al. (1987) |
| Grey relational analysis |
Deng (1989) |
| Analytic network process (ANP) |
Saaty (1996) |
| VIKOR |
Opricovic (1998) |
| Superiority and inferiority ranking (SIR) |
Xu (2001) |
| PAPRIKA |
Hansen and Ombler (2008) |
| Best‐worst method (BWM) |
Rezaei et al. (2015) |
| Weighting Methods |
Entropy method |
Shannon (1948) |
| Delphi method |
Dalkey and Helmer (1963) |
| Eigenvector method |
Saaty (1977) |
| Weighted least square method |
Chu et al. (1979) |
| Multiple objective programming model |
Choo and Wedley (1985) |
| Principal element analysis |
Fan (1996) |
| Modified Delphi method |
Custer et al. (1999) |
Almost everyone, on a daily bases, faces decision‐making problems. It would not be exaggerated to state that these decisions constitute the nature of mankind and of the society that humans form. When it comes to real‐world decision‐making problems, the decision‐makers often find judgment a challenging task. This is so because of the notion that the interest of the stakeholders can be only represented through the evaluation of a set of conflictive criteria. Whenever the decision‐makers face a set of feasible, discrete, alternatives, the problem at hand involves MADM. Numerous methods have been presented by been reported to ensure a sound and reliable decision‐making process. MADM is one of the main branches of operational research; it is an active field of study with multiple overlaps with many scientific disciplines, and has numerous practical applications. This chapter reviewed the principles of MADM. Furthermore, the best well‐known MADMs were herein classified and reviewed.
1 Banihabib, M.E., Hashemi‐Madani, F.S., and Forghani, A. (2017). Comparison of compensatory and non‐compensatory multi criteria decision making models in water resources strategic management. Water Resources Management 31 (12): 3745–3759.
2 Bell, D.E., Raiffa, H., and Tversky, A. (1988). Decision Making: Descriptive, Normative, and Prescriptive Interactions. Cambridge, UK: Cambridge University Press.
3 Bellman, R.E. and Zadeh, L.A. (1970). Decision‐making in a fuzzy environment. Management Science 17 (4): 141–164.
4 Belton, V. and Stewart, T. (2002). Multiple Criteria Decision Analysis: An Integrated Approach. Massachusetts, BST: Kluwer Academic Publishers.
5 Benayoun, R., Roy, B., and Sussman, B. (1966). ELECTRE: Une méthode pour guider le choix en présence de points de vue multiples. Note de travail 49, SEMA‐METRA International, Direction Scientifique, Paris, France.
6 Bernstein, P. (1996). Against the Gods: The Remarkable Story of Risk. New York, NY: Wiley.
7 Bernoulli, D. (1738). Specimen theoriae novae de mensura sortis. Comentarii Academiae Scientiarum Imperiales Petropolitanae 1738 (5): 175–192.
8 Black, D. (1948). On the rationale of group decision‐making. Journal of Political Economy 56 (1): 23–34.
9 Bozorg‐Haddad, O., Solgi, M., and Loáiciga, H.A. (2017). Meta‐heuristic and Evolutionary Algorithms for Engineering Optimization. Hoboken, NJ: Wiley.
10 Brans, J.P. (1982). L’ingénierie de la decision. Elaboration d’instruments d’aide a la decision: Methode PROMETHEE. In: L’aide a la Decision: Nature, Instruments et Perspectives D’avenir (eds. R. Nadeau and M. Landry), 183–214. Québec, Canada: Presses de Universite Laval.
11 Brans, J.P., Vincke, P., and Mareschal, B. (1986). How to select and how to rank projects: the PROMETHEE method. European Journal of Operational Research 24 (2): 228–238.
12 Choo, E.U. and Wedley, W.C. (1985). Optimal criterion weights in repetitive multicriteria decision‐making. Journal of the Operational Research Society 36 (11): 983–992.
13 Chu, A.T.W., Kalaba, R.E., and Spingarn, K. (1979). A comparison of two methods for determining the weights of belonging to fuzzy sets. Journal of Optimization Theory and Applications 27 (4): 531–538.
14 Churchman, C.W. and Ackoff, R.L. (1954). An approximate measure of value. Journal of the Operations Research Society of America 2 (2): 172–187.
15 Coombs, C.H. and Pruitt, D.G. (1960). Components of risk in decision making: probability and variance preferences. Journal of Experimental Psychology 60 (5): 265.
Читать дальше