Daniel J. Denis - Applied Univariate, Bivariate, and Multivariate Statistics

The first point is that statistics is not mathematics. Statistics is a discipline unto itself that usesmathematics, the way physics uses mathematics, and the way that virtually all of the natural and social sciences use mathematics. Mathematics is the tool statisticians use to express their statistical ideas, and statistics is the tool that scientists use to help make sense of their research findings. The field of theoreticalor mathematical statisticsis heavily steeped in theorem‐building and proofs. Applied statistics, of the kind featured in this book, is definitely not. Thus, any fear of real mathematicscan be laid to rest, because you will find no such mathematics in this book. Upon browsing this book, if you are of the opinion that it contains “lots of math,” then quite simply, you do not know what “lots of math” looks like. Rest assured, the mathematics in this book is simply used as a vehicle for understanding statistics.

Mathematics and statistics are not things “mysterious” that can only be grasped by those with higher mental faculties. A useful working definition might be that mathematics is a set of well‐defined and ever‐expanding rulesand consequences about symbolic abstract objects based on fundamental assumptions called axioms. The axioms of mathematics are typically assumed to be true without needing to be proved. Theorems and other results built on such axioms usually require proof. What is a proof? It is an analytical argument for why a proposition should be considered true. Any given proof usually relies on other theorems that have already been proven to be true. Make no mistake, mathematics is a very deep field of intellectual endeavor and activity. However, expecting something to be deeper than it is can also lead you to just as well not understand it. Sometimes, if you are not understanding something, it may very well be that you are looking far beyond what there is to be understood. If you retreat in your expectations slightly of what there is to see, it sometimes begins to make more sense. Thinking “too deep” where such depth is not required or encouraged, is a peril. Many “bright” students have this “gift” of critical analysis, and to understand a concept, need to actually retreat somewhat in their depth of inquiry (at least for the moment).

For a general overview of the nature of mathematics, the reader is encouraged to consult Courant, Robbins, and Stewart (1996), and for an excellent introduction to basic mathematical analysis, Labarre (1961). Hamming (1985) is another good introduction to the field of mathematics, as well as Aleksandrov, Kolmogorov, and Lavrent’ev (1999). For more philosophical treatments, the reader should consult Dunham (1994) and Stewart (1995). For an in‐depth and very readable history of mathematics, consult Boyer and Merzbach (1991).

The answer to this question is, of course, as much as possible, for working through problems of any kind can only serve to hone your analytical and deductive abilities. Even working through problems completely unrelated to statistics can help your statistical abilities, because they give you practice in “figuring things out.” However, that answer is, of course, a naïve if not idealistic one, since there is only so much time available for study and the study of statistics must be balanced by your own study of your chosen field.

For example, if the biology student became immersed in mathematics and statistics full‐time, then that student would no longer be a student of biology. It can be exceedingly difficult to apply a statistical technique and interpret the results of such a technique in a field for which you are not familiar. If you are unaware of the substantive objects you are working with, that is, the “stuff” on which the statistics are being applied, then regardless of your quantitative expertise, you will often have difficulty interpreting the scientific result. Likewise, if spending too much time computing higher‐order derivatives, the student of animal learning, for instance, will have little time remaining to study the learning patterns of the rats he is conditioning, or to speculate on theoretical advancements in his field. Hence, a “happy medium” is required that will balance your study of your substantive area along with the technical quantitative demands of your field of study. Indeed, even for those who specialize exclusively in statistics, the American Statistical Associationstrongly advises aspiring statisticians to choose a field of application. As a researcher, you will be expected to apply modeling techniques that are quite advanced (entire courses are devoted to the statistical technique you may be applying), and so you will face the opposite problem, that of choosing to specialize in statistics (to some extent) so that you may better understand the phenomena of your own science. Hence, regardless of whether one is coming from a mathematics or science background, one should aspire for a healthy mix of scientific and statistical expertise. Computingexperience (e.g., R, SPSS, SAS, etc.) should also be part of your “repertoire” of skills. As an applied scientist, you should probably find yourself in the data scienceor traditional researchintersections in the following Venn diagram.

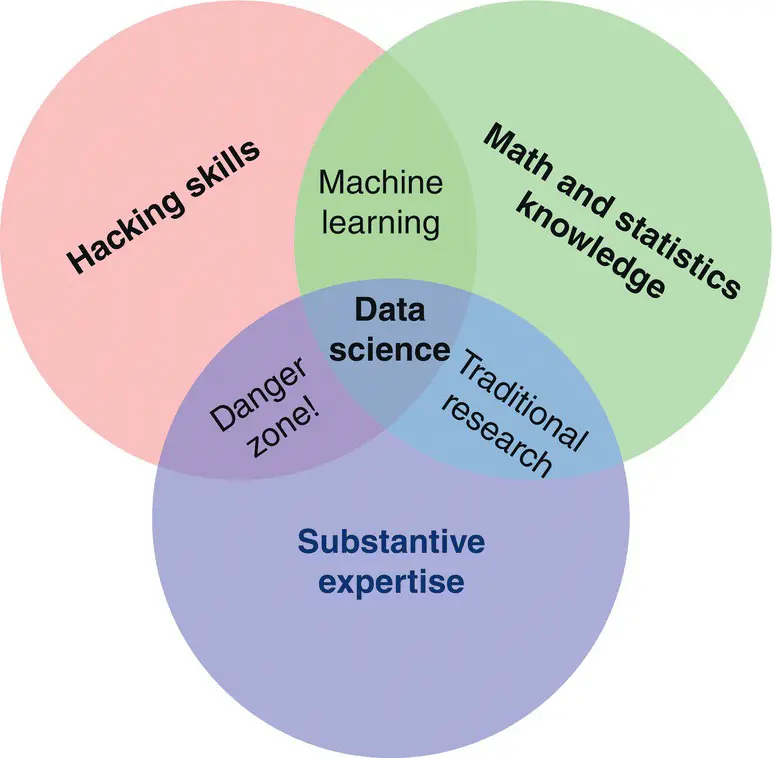
Source: From Drew Conway, THE DATA SCIENCE VENN DIAGRAM, Sep 30, 2010. Reproduced with permission from Drew Conway.

Statistical thinking is all about relativity. Statistics are not about numbers, they are about distributionsof numbers (Green, 2000, personal communication). Rarely in statistics, or science for that matter, do we evaluate things in a vacuum.

Consider a very easy example. You board an airplane destined to your favorite vacation spot. How talented is the pilot who is flying your airplane? Is he a “good” pilot or a “bad” pilot? One would hope he is “good enough” to fulfill his duties and ensure your and other passengers' safety. However, when you start thinking like a statistician, you may ponder the thought of how good of a pilot he is relative to other pilots. Where on the curve does your pilot fall? In terms of his or her skill, the pilot of an airplane can be absolutelygood, but still relativelypoor. Perhaps that pilot falls on the lower end of the talent curve for pilots. The pilot is still very capable of flying the plane, they have passed an absolute standard, but he or she just isn't quite as good as most other pilots (see Figure 1.5).

We can come up with a lot of other examples to illustrate the absoluteversus relativedistinction. If someone asked you whether you are intelligent, ego aside, as a statistician, you may respond “relative to who?” Indeed, with a construct like IQ, relativity is all we really have. What does absolute intelligencelook like? Should our species discover aliens on another planet one day, we may need to revise our definition of intelligence if such are much more (or much less) advanced than we are. Though of course, this would assume we have the intelligence to comprehend that their capacities are more than ours, a fact not guaranteed and hence another example of the trap of relativity.