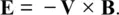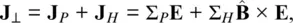(2.1) 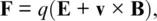
such that the momentum equation for individual ions and electrons is
(2.2) 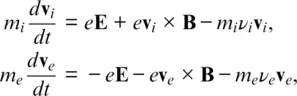
where we consider singly charged positive ions for simplicity (mainly protons in the magnetosphere and heavier ions such as O +and O 2 +in the ionosphere), we have used q = e and q = − e for ions and electrons, and the last terms on the RHS represent momentum loss due to collisions with a background of uncharged particles, such as the atmosphere, with collision rates (frequencies) ν iand ν e. We assume initially that ν i= ν e= 0.
In a situation with no electric field, E= 0, and uniform magnetic field B, the momentum equations can be solved to show that the magnetic force causes particles to move in a circle in a plane perpendicular to B( Fig. 2.4a), of radius r gwith angular frequency Ω, where
(2.3) 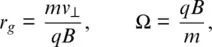
the gyration being in a right‐handed sense about the field direction if q < 0 and left‐handed if q > 0. In a given field strength B , the gyroradius depends on the speed of the particle perpendicular to the magnetic field, v ⊥, such that the gyrofrequency is the same for all particles of a particular species (that is, with a given charge to mass ratio 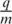 ). Hotter plasma (a larger range of v ⊥) will tend to have larger gyroradii. In a uniform magnetic field, the particles experience no force along the magnetic field direction, their initial parallel speed v ‖is unchanged, and, in general, they are highly mobile along magnetic field lines. Each particle forms a current loop, but in a uniform plasma, the currents of adjacent particles cancel out. However, where there are gradients in plasma density or temperature (and hence pressure), a net magnetization current can flow. If the magnetic field has a gradient along its length, as shown in Figure 2.4d, then q v× Bhas a component that modifies v ‖and expels particles from high‐field regions. In this way, particles are kept away from the Earth by this “mirror force” (see converging Bregions near the Earth in Fig. 2.2) and tend to be trapped within the magnetosphere. Gradients in field strength perpendicular to B, such as in the Earth's inner dipole, lead to variations in gyroradius that cause charge‐dependent “gradient drift” and hence an electric current to flow ( Fig. 2.4e). Gradient drift is enhanced by the curvature of the dipole field. This combined “gradient‐curvature drift” is significant for hot plasma with large gyroradii and rapid field‐parallel motions.
). Hotter plasma (a larger range of v ⊥) will tend to have larger gyroradii. In a uniform magnetic field, the particles experience no force along the magnetic field direction, their initial parallel speed v ‖is unchanged, and, in general, they are highly mobile along magnetic field lines. Each particle forms a current loop, but in a uniform plasma, the currents of adjacent particles cancel out. However, where there are gradients in plasma density or temperature (and hence pressure), a net magnetization current can flow. If the magnetic field has a gradient along its length, as shown in Figure 2.4d, then q v× Bhas a component that modifies v ‖and expels particles from high‐field regions. In this way, particles are kept away from the Earth by this “mirror force” (see converging Bregions near the Earth in Fig. 2.2) and tend to be trapped within the magnetosphere. Gradients in field strength perpendicular to B, such as in the Earth's inner dipole, lead to variations in gyroradius that cause charge‐dependent “gradient drift” and hence an electric current to flow ( Fig. 2.4e). Gradient drift is enhanced by the curvature of the dipole field. This combined “gradient‐curvature drift” is significant for hot plasma with large gyroradii and rapid field‐parallel motions.

Figure 2.4 Schematic of (a) gyrating particles, (b) E× Bdrifting particles, (c) E× Bdrifting particles in the presence of neutrals, (d) particles mirroring in a high field region, and (e) a gradient in Bproducing charge‐dependent drift.
If the magnetic field is uniform, and an electric field is introduced ( Fig. 2.4b), charged particles initially at rest are accelerated by the electric force, caused to deviate by the magnetic force, and then are decelerated by the electric force, performing a half gyration before coming to a rest again. The cycle repeats, and the particles follow cycloid trajectories with an average bulk drift in the E× Bdirection with a speed E / B E/B, that is a velocity
(2.4) 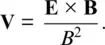 (2.4)
(2.4)
An observer moving with the plasma would just see circular gyrations (as in Fig. 2.4a), the trajectories that are expected in the presence of a magnetic field but no electric field. This demonstrates that the electric field is dependent on one's frame of reference, a consequence of the theory of special relativity, and in a frame in which a magnetized plasma is drifting with velocity V, a motional electric field Eexists, where
(2.5) 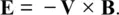
The above discussion is appropriate for the magnetosphere and F region ionosphere, where collisions can be discounted. Figure 2.4c shows how Figure 2.4b must be modified in the E and D region ionosphere where a dense background of neutrals exists, such that the collisional terms of equation (2.2)become significant. As the particles E× Bdrift, they are occasionally brought to a rest by collisions, before being re‐accelerated by the electric field. The particles' drift motion in the E× Bdirection is slowed by the collisions, and ions and electrons acquire an additional drift parallel and antiparallel to E, respectively, resulting in bulk drifts of V iand V e. This differential drift represents a current, j(A m −2), where j = e ( n i V i − n e V e) and n iand n eare the number densities of ions and electrons. The current has components in the − E× Band + Edirections, known as the Hall and Pedersen currents, j Hand j P, respectively. In the polar ionosphere, where Bis directed vertically, these currents flow horizontally. The magnitude of these currents depends on E, on the electron density, and on the ion‐neutral and electron‐neutral collision frequencies, ν iand ν e, which are altitude dependent. In the F region, where collisions are rare, the ionospheric plasma undergoes E× Bdrift, in the E region significant currents flow, and in the D region collisions are so prevalent that plasma motions and hence currents are negligible. Integrating in height through the ionosphere, total horizontal currents J Hand J Phave associated conductances ∑ Hand ∑ P, which mainly depend on E region electron density, and hence are largest in the sunlit ionosphere and the auroral zones. The ionospheric (i.e., field‐perpendicular) current J ⊥(A m −1) driven in the presence of an electric field Eis
(2.6) 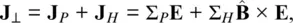
Читать дальше

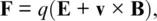
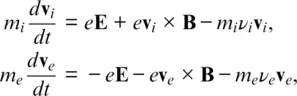
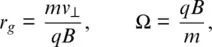
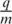 ). Hotter plasma (a larger range of v ⊥) will tend to have larger gyroradii. In a uniform magnetic field, the particles experience no force along the magnetic field direction, their initial parallel speed v ‖is unchanged, and, in general, they are highly mobile along magnetic field lines. Each particle forms a current loop, but in a uniform plasma, the currents of adjacent particles cancel out. However, where there are gradients in plasma density or temperature (and hence pressure), a net magnetization current can flow. If the magnetic field has a gradient along its length, as shown in Figure 2.4d, then q v× Bhas a component that modifies v ‖and expels particles from high‐field regions. In this way, particles are kept away from the Earth by this “mirror force” (see converging Bregions near the Earth in Fig. 2.2) and tend to be trapped within the magnetosphere. Gradients in field strength perpendicular to B, such as in the Earth's inner dipole, lead to variations in gyroradius that cause charge‐dependent “gradient drift” and hence an electric current to flow ( Fig. 2.4e). Gradient drift is enhanced by the curvature of the dipole field. This combined “gradient‐curvature drift” is significant for hot plasma with large gyroradii and rapid field‐parallel motions.
). Hotter plasma (a larger range of v ⊥) will tend to have larger gyroradii. In a uniform magnetic field, the particles experience no force along the magnetic field direction, their initial parallel speed v ‖is unchanged, and, in general, they are highly mobile along magnetic field lines. Each particle forms a current loop, but in a uniform plasma, the currents of adjacent particles cancel out. However, where there are gradients in plasma density or temperature (and hence pressure), a net magnetization current can flow. If the magnetic field has a gradient along its length, as shown in Figure 2.4d, then q v× Bhas a component that modifies v ‖and expels particles from high‐field regions. In this way, particles are kept away from the Earth by this “mirror force” (see converging Bregions near the Earth in Fig. 2.2) and tend to be trapped within the magnetosphere. Gradients in field strength perpendicular to B, such as in the Earth's inner dipole, lead to variations in gyroradius that cause charge‐dependent “gradient drift” and hence an electric current to flow ( Fig. 2.4e). Gradient drift is enhanced by the curvature of the dipole field. This combined “gradient‐curvature drift” is significant for hot plasma with large gyroradii and rapid field‐parallel motions.
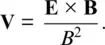 (2.4)
(2.4)