Nanometer-scale Defect Detection Using Polarized Light focused on three levels of design for manufacturing an industrial product:
– Numerical methods developed in engineering from mathematical models and theories in order to optimize product quality from its design according to RBDO. This methodology is a source of applications in engineering science intended to address optimization problems in the industrial field.
– Experimental methods developed in fundamental research relying on the light–matter interaction and on simulation-based analysis using theoretical models in order to make nanometer-scale measurements and conduct the analysis. These methods are used in nanosciences for the elaboration of knowledge leading to nanotechnologies.
– Finally, the application of these two approaches in the example presented in Chapter 9 of Nanometer-scale Defect Detection Using Polarized Light to the measurement of the physical properties of a nanomaterial, carbon nanotube.
In sciences, there are various ways to measure a dimension. The measuring instruments or methods employed depend on the scale at which metrology is approached. In order to describe the issues at stake for measurement at a given scale, we present the methods employed for the measurement processes at two scales of interest for scientists, namely the infinitely small, which corresponds to the Planck length of 1.6 x 10 –35m, and the infinitely large, which corresponds to the diameter of the Universe evaluated at 8.8 x 10 26m. This is to help the reader understand that, even though becoming an expert in a scientific field or in a given subject is not the objective, it is necessary to understand some basic tenets in order to master the methods used for successful metrology at a given scale.
In 1899, Planck determined a unit of length 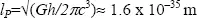 , referred to as Planck length, based on fundamental constants: G , gravitational constant (6.6 x 10 –11Nm 2Kg –2), h , Planck’s constant (6.64 x 10 –34Js) and c , the speed of light (2.99,729,458 x 10 8ms –1). This length cannot be measured with the measurement technologies available on Earth. Indeed, the smallest length measurable at the LHC (Large Hadron Collider) of CERN, the particle accelerator in which two protons are made to frontally collide in a ring of 26,659 km, which led to the discovery in 2012 of the Higgs boson, is approximately 10 –16m, which is 19 orders of magnitude higher than the Planck length. CMS and ATLAS detectors were used in the observation of the Higgs boson, the latest prediction of the standard model not yet observed. The measurement at the scale of 10 –16m is made by compressing energy to reach an infinitely small spatial volume.
, referred to as Planck length, based on fundamental constants: G , gravitational constant (6.6 x 10 –11Nm 2Kg –2), h , Planck’s constant (6.64 x 10 –34Js) and c , the speed of light (2.99,729,458 x 10 8ms –1). This length cannot be measured with the measurement technologies available on Earth. Indeed, the smallest length measurable at the LHC (Large Hadron Collider) of CERN, the particle accelerator in which two protons are made to frontally collide in a ring of 26,659 km, which led to the discovery in 2012 of the Higgs boson, is approximately 10 –16m, which is 19 orders of magnitude higher than the Planck length. CMS and ATLAS detectors were used in the observation of the Higgs boson, the latest prediction of the standard model not yet observed. The measurement at the scale of 10 –16m is made by compressing energy to reach an infinitely small spatial volume.
The principle of measurement at the scale of fundamental particles is mainly based on three relations: the de Broglie relation between the momentum p and the wavelength λ, p=h /λ, which introduces the wave–particle duality for matter; the relation that links the energy E of a particle to its wave frequency or wavelength λ, such as proposed by Einstein to explain the photoelectric effect E = hc /λ; and the relation that links the energy E of a particle of rest mass m to its rest mass energy and to its kinetic energy associated with its momentum p=mv , E 2= m 2c 4+ p 2c 2, as mentioned in Einstein’s special theory of relativity. In the above formulas, v is the speed of the particle of mass m and c is the speed of light. The energy E can also be expressed by the formula E = γ mc 2, where γ is given by 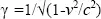 . The speed of a particle is therefore given by
. The speed of a particle is therefore given by 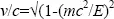 .
.
In the LHC, the energy of a proton is 7 TeV (1.2 10 –6J), far higher (by a factor of 7,500) than its rest energy, mc 2, which is 938 MeV. The formula for speed can then be rewritten as v/c = (1-( m2c 4/2 E 2)), which is equal to 1 to the nearest 10 –8. Using the relation E = hc/λ , the resulting value of the wavelength is of the order of 10 –16m, which gives the dimensions that can be reached in the LHC. The mass measured during two experiments at CERN in the LHC (8 TeV in 2012 and 13 TeV in 2015) is confirmed to the value of 125 GeV.
To detect the Higgs boson, a particle of mass 125 GeV associated with the Higgs field, while the mass of a proton is 938 MeV, the proton is accelerated and consequently its kinetic energy is increased so that its energy given by E = γ mc 2significantly exceeds 938 MeV (8 TeV in 2012 and 13 TeV in 2015). The disintegration of colliding protons, each contributing an energy load of 8 TeV or 13 TeV, releases sufficient energy so that the Higgs boson can be expected to emerge during the recombination of subatomic particles. As the Higgs boson decays quasi-instantaneously after its emergence, the products of its decay must be analyzed to identify the excess energy and therefore the excess mass about 125 GeV.
It is worth noting that at the Planck length, the required energies that cannot be expected in a particle accelerator would lead to the emergence of black holes.
The opposite dimensional extreme towards the infinitely large corresponds to the spatial extent of the Universe, whose estimated value according to cosmologists is 10 26m. In cosmology, the observable Universe is a term used to describe the visible part of our Universe, the point from which light reaches us. It is a sphere whose limit is located at the cosmological horizon, having the Earth at its center. It is therefore a relative notion, as for other observers located somewhere else in the Universe, the observable sphere would not be the same (while its radius would be identical).
In cosmology, distances are measured in light-years. A light-year is the distance that light travels in one year, which corresponds to approximately 9.5 x 10 12m. The megaparsec, which is 3.26 million (3.26 x 10 6) light-years, is another unit of distance that is also specific to extragalactic astrophysics. Finding the size of the Universe involves accurate measurements of fossil radiation, or of the cosmic microwave background (CMB) radiation that originated in the Big Bang and can be used to determine the volume filled by the Universe since its creation. Predicted for the first time by Ralph Alpher in 1948 in his thesis work, CMB was discovered by Arno Penzias and Robert Wilson at “Bell Telephone Laboratories” during the development of a new radio receiver following the interferences detected independently of the orientation of the antenna they were building. While in a first approximation CMB is isotropic, accurate measurements of this radiation lead to determining H 0, the Hubble constant, which indicates the rate of expansion of the Universe.
In cosmology, detectors are above-ground telescopes. The WMAP (Wilkinson Microwave Anisotropy Probe) satellite launched in 2001 enabled the detection of CMB with good accuracy. Its intensity varies slightly in different directions of the sky and the fluctuations can be determined. Extremely accurate measurements of the WMAP in 2003 made it possible to calculate a value of H 0of 70 kilometers per second and per megaparsec, which is within 5% in the hypothesis of a constant rate of expansion. Since the Universe is accelerating, during its expansion, the correction brought to H 0made it possible to estimate the age of the Universe to 13.75 billion years, with a 0.1 billion margin of error. It is the scale fitting the domain to which corresponds the age of the Universe deduced from observations related to the Big Bang based on the inflationary model in an expanding Universe.
Читать дальше

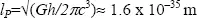 , referred to as Planck length, based on fundamental constants: G , gravitational constant (6.6 x 10 –11Nm 2Kg –2), h , Planck’s constant (6.64 x 10 –34Js) and c , the speed of light (2.99,729,458 x 10 8ms –1). This length cannot be measured with the measurement technologies available on Earth. Indeed, the smallest length measurable at the LHC (Large Hadron Collider) of CERN, the particle accelerator in which two protons are made to frontally collide in a ring of 26,659 km, which led to the discovery in 2012 of the Higgs boson, is approximately 10 –16m, which is 19 orders of magnitude higher than the Planck length. CMS and ATLAS detectors were used in the observation of the Higgs boson, the latest prediction of the standard model not yet observed. The measurement at the scale of 10 –16m is made by compressing energy to reach an infinitely small spatial volume.
, referred to as Planck length, based on fundamental constants: G , gravitational constant (6.6 x 10 –11Nm 2Kg –2), h , Planck’s constant (6.64 x 10 –34Js) and c , the speed of light (2.99,729,458 x 10 8ms –1). This length cannot be measured with the measurement technologies available on Earth. Indeed, the smallest length measurable at the LHC (Large Hadron Collider) of CERN, the particle accelerator in which two protons are made to frontally collide in a ring of 26,659 km, which led to the discovery in 2012 of the Higgs boson, is approximately 10 –16m, which is 19 orders of magnitude higher than the Planck length. CMS and ATLAS detectors were used in the observation of the Higgs boson, the latest prediction of the standard model not yet observed. The measurement at the scale of 10 –16m is made by compressing energy to reach an infinitely small spatial volume.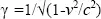 . The speed of a particle is therefore given by
. The speed of a particle is therefore given by 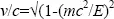 .
.










