William Kinlaw - Asset Allocation

We combine our objective and constraints to form the following objective function:

(2.3)

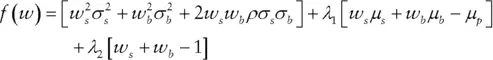
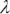The first term of Equation 2.3up to the third plus sign equals portfolio variance, the quantity to be minimized. The next two terms that are multiplied by represent the two constraints. The first constraint ensures that the weighted average of the stock and bond returns equals the portfolio's expected return. The Greek letter lambda ( 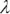) is called a Lagrange multiplier. It is a variable introduced to facilitate optimization when we face constraints, and it does not easily lend itself to economic interpretation. The second constraint guarantees that the portfolio is fully invested. Again, lambda serves to facilitate a solution.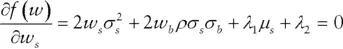

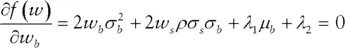
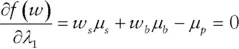
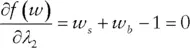
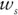Our objective function has four unknown values: (i) the percentage of the portfolio to be allocated to stocks, (ii) the percentage to be allocated to bonds, (iii) the Lagrange multiplier for the first constraint, and (iv) the Lagrange multiplier for the second constraint. To minimize portfolio risk given our constraints, we must take the partial derivative of the objective function with respect to each asset weight and with respect to each Lagrange multiplier and set it equal to zero, as shown below:

(2.4)

(2.5)

(2.6)

(2.7)

Given assumptions for expected return, standard deviation, and correlation (which we specify later), we wish to find the values of and 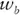associated with different values of 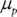, the portfolio's expected return. The values for 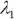and 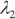are merely mathematical by-products of the solution.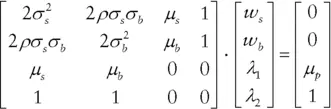

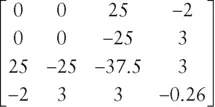
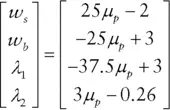
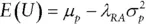
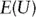Next, we express Equations 2.4, 2.5, 2.6, and 2.7in matrix notation, as follows:

(2.8)

We next substitute estimates of expected return, standard deviation, and correlation for domestic equities and Treasury bonds shown earlier in Tables 2.1and 2.2.

With these assumptions, we rewrite the coefficient matrix as follows:

Its inverse equals:

Because the constant vector includes a variable for the portfolio's expected return, we obtain a vector of formulas rather than values when we multiply the inverse matrix by the vector of constants, as follows:

(2.9)

We are interested only in the first two formulas. The first formula yields the percentage to be invested in stocks in order to minimize risk when we substitute a value for the portfolio's expected return. The second formula yields the percentage to be invested in bonds. Table 2.3shows the allocations to stocks and bonds that minimize risk for portfolio expected returns ranging from 9% to 12%.

TABLE 2.3Optimal Allocation to Stocks and Bonds

In 1987, William Sharpe published an algorithm for portfolio optimization that has the dual virtues of accommodating many real-world complexities while appealing to our intuition. 8 We begin by defining an objective function that we wish to maximize:

(2.10)

In Equation 2.8, equals expected utility, 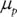equals portfolio expected return, 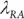equals risk aversion, and 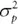equals portfolio variance.

Utility is a measure of well-being or satisfaction, whereas risk aversion measures how many units of expected return we are willing to sacrifice in order to reduce risk (variance) by one unit. ( Chapter 25includes more detail about utility and risk aversion.) By maximizing this objective function, we maximize expected return minus a quantity representing our aversion to risk times risk (as measured by variance).

Again, assume we have a portfolio consisting of stocks and bonds. Substituting the equations for portfolio expected return and variance ( Equations 2.1and 2.2), we rewrite the objective function as follows:

(2.11)

This objective function measures the expected utility or satisfaction we derive from a combination of expected return and risk, given our attitude toward risk. Its partial derivative with respect to each asset weight, shown in Equations 2.12and 2.13, represents the marginal utility of each asset class:

(2.12)