Figure 4.3.
Illustration of spectral transform design methodology. Traditional methods use a sample covariance to derive an approximation of KLT (sample KLT). This chapter focuses on approaches to find a graph Laplacian from data for designing GFTs (whose steps are represented by red arrows). For a color version of this figure, see www.iste.co.uk/cheung/graph.zip Figure 4.4.
2D GMRF models for intra- and inter-predicted signals. Filled vertices correspond to reference pixels obtained (a) from neighboring blocks and (b) from other frames via motion compensation. Unfilled vertices denote the pixels to be predicted and then transform coded. This figure is adapted from Figure 3 in Egilmez et al. (2020a) Figure 4.5.
1D GMRF models for (a) intra- and (b) inter-predicted signals. Black-filled vertices represent the reference pixels and unfilled vertices denote pixels to be predicted and then transform coded. This figure is adapted from Figure 2 in Egilmez et al. (2020a) Figure 4.6.
An illustration of graph construction for a given 8 × 8 residual block signal, where wc = 1 and we = wc/sedge = 0.1 where sedge = 10. The resulting basis patches are also depicted. For a color version of this figure, see www.iste.co.uk/cheung/graph.zip Figure 4.7.
A 1D graph-based model with an image edge at location l = j. All black colored edges have weights equal to wc, and the gray edge between vertices vj and vj+1 is weighted as we = wc/sedge. This figure is adapted from Figure 5 in Egilmez et al. (2020a) Figure 4.8.
Coding gain (cg) versus sedge for block sizes with N = 4, 8, 16, 32, 64. EA-GFT provides better coding gain (i.e. cg is negative) when sedge is larger than 10 across different block sizes. This figure is adapted from Figure 6 in Egilmez et al. (2020a). For a color version of this figure, see www.iste.co.uk/cheung/graph.zip Figure 4.9.
Coding gain (cg) versus bits per pixel (R/N) for different edge sharpness parameters sedge = 10, 20, 40, 100, 200. EA-GFT provides better coding gain (i.e. cg is negative) if sedge is larger than 10 for different block sizes. This figure is adapted from Figure 7 in Egilmez et al. (2020a). For a color version of this figure, see www.iste.co.uk/cheung/graph.zip Figure 4.10.
BD-rates achieved for coding intra-predicted blocks with the RDOT scheme based on KLT, S-GFT and NS-GFT, which are trained on datasets with fewer number of samples. This figure is adapted from Figure 14 in Egilmez et al. (2020a). For a color version of this figure, see www.iste.co.uk/cheung/graph.zip
6 Chapter 5Figure 5.1. Example of a 3D point cloud: Stanford Bunny. For a color version of this figure, see www.iste.co.uk/cheung/graph.zip Figure 5.2. Example of omnidirectional image: Sopha (Hawary et al. 2020). For a color version of this figure, see www.iste.co.uk/cheung/graph.zip Figure 5.3. Example of light field image: Succulents ( Jiang et al. 2017 ). For a color version of this figure, see www.iste.co.uk/cheung/graph.zip Figure 5.4. General scheme of graph spectral 3D image compression Figure 5.5. Graph-based encoder’s principles, where x is the signal to encode, ŷ is the previously decoded data, z is the residue, α the transformed coefficients and 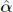 their quantized version Figure 5.6. Illustration of the difference between a compact and a not compact representation. For a color version of this figure, see www.iste.co.uk/cheung/graph.zip Figure 5.7. Graph topology for light fields and multi-view images. For a color version of this figure, see www.iste.co.uk/cheung/graph.zip Figure 5.8. Graph topology for point clouds. For a color version of this figure, see www.iste.co.uk/cheung/graph.zip Figure 5.9. Graph topology for omnidirectional images based on two different sampling approaches. For a color version of this figure, see www.iste.co.uk/cheung/graph.zip Figure 5.10. Example of a rate-distortion optimized graph partition in an omnidirectional image. Left: in the equirectangular domain; right: in the sphere domain. For a color version of this figure, see www.iste.co.uk/cheung/graph.zip Figure 5.11. Illustration of the output of the optimization process for a super-ray in four views of a light field. The first row corresponds to a super-ray across four views of the light field. The signal on the vertices corresponds to the color values lying on super-pixels corresponding to the same super-ray and the blue lines denote the correspondences based on the geometrical information in hand. The second to fourth rows are illustrations of basis functions before and after optimization. The signals on the vertices are the eigenvectors values. For a color version of this figure, see www.iste.co.uk/cheung/graph.zip
their quantized version Figure 5.6. Illustration of the difference between a compact and a not compact representation. For a color version of this figure, see www.iste.co.uk/cheung/graph.zip Figure 5.7. Graph topology for light fields and multi-view images. For a color version of this figure, see www.iste.co.uk/cheung/graph.zip Figure 5.8. Graph topology for point clouds. For a color version of this figure, see www.iste.co.uk/cheung/graph.zip Figure 5.9. Graph topology for omnidirectional images based on two different sampling approaches. For a color version of this figure, see www.iste.co.uk/cheung/graph.zip Figure 5.10. Example of a rate-distortion optimized graph partition in an omnidirectional image. Left: in the equirectangular domain; right: in the sphere domain. For a color version of this figure, see www.iste.co.uk/cheung/graph.zip Figure 5.11. Illustration of the output of the optimization process for a super-ray in four views of a light field. The first row corresponds to a super-ray across four views of the light field. The signal on the vertices corresponds to the color values lying on super-pixels corresponding to the same super-ray and the blue lines denote the correspondences based on the geometrical information in hand. The second to fourth rows are illustrations of basis functions before and after optimization. The signals on the vertices are the eigenvectors values. For a color version of this figure, see www.iste.co.uk/cheung/graph.zip
7 Chapter 6Figure 6.1. Several representative image restoration problems. The bottom-middle image is the original image. For a color version of this figure, see www.iste.co.uk/cheung/graph.zip Figure 6.2. A simple grid graph . This figure has only showed a part of the graph. For a color version of this figure, see www.iste.co.uk/cheung/graph.zip Figure 6.3. Denoising results of different approaches, with depth map Teddy corrupted by AWGN(σ=10). © 2013 IEEE. Reprinted, with permission, from Hu et al.(2013) Figure 6.4. Illustrations of different kinds of images.(a) A true natural image,(b) a blurry image,(c) a skeleton image, and(d),(e) and(f) are patches in the green squares of(a),(b) and(c), respectively. © 2018 IEEE. Reprinted, with permission, from Bai et al.(2019). For a color version of this figure, see www.iste.co.uk/cheung/graph.zip Figure 6.5. Edge weight distribution around image edges.(a) A true natural patch,(b) a blurry patch, and(c) a skeleton patch. © 2018 IEEE. Reprinted, with permission, from Bai et al.(2019). For a color version of this figure, see www.iste.co.uk/cheung/graph.zip Figure 6.6. Deblurring results comparison.(a) Blurry image.(b) Sun et al.(2013).(c) Michaeli and Irani(2014).(d) Lai et al.(2015).(e) Pan et al.(2016).(f) RGTV. The blur kernel is shown at the lower left corner. © 2018 IEEE. Reprinted, with permission, from Bai et al.(2019). For a color version of this figure, see www.iste.co.uk/cheung/graph.zip Figure 6.7. (a) A patch being optimized encloses a smaller code block. Boundary discontinuity is removed by averaging overlapping patches.(b) The relationship between the dictionary size and the restoration performance. © 2016 IEEE. Reprinted, with permission, from Liu et al.(2017). For a color version of this figure, see www.iste.co.uk/cheung/graph.zip Figure 6.8. Comparison with competing schemes on Butterfly at QF = 5. The corresponding PSNR and SSIM values are shown © 2016 IEEE. Reprinted, with permission, from Liu et al.(2017) Figure 6.9. Sampling the exemplar function fn at pixel locations in domain Ω. © 2017 IEEE. Reprinted, with permission, from Pang and Cheung(2017). For a color version of this figure, see www.iste.co.uk/cheung/graph.zip Figure 6.10. (a) –(c) Different scenarios of using the metric norm as a “pointwise” regularizer.(d) The ideal metric space. The red dots mark the ground-truth gradient. © 2017 IEEE. Reprinted, with permission, from Pang and Cheung(2017). For a color version of this figure, see www.iste.co.uk/cheung/graph.zip Figure 6.11. Denoising of the image Lena, where the original image is corrupted by AWGN with σI = 40. Two cropped fragments of each image are presented for comparison. © 2017 IEEE. Reprinted, with permission, from Pang and Cheung(2017) Figure 6.12. Inpainting of the image Peppers with the low-dimensional manifold model(LDMM), where the corrupted image only keeps 10% of the pixels from the original imageFigure 6.13. Results of real image denoising.(a) Noise clinic(model-based)(Lebrun et al. 2015);(b) CDnCNN(data-driven)(Zhang et al. 2017);(c) DeepGLR. CDnCNN and DeepGLR are trained for Gaussian denoising. ©2019 IEEE. Reprinted, with permission, from Zeng et al.(2019). For a color version of this figure, see www.iste.co.uk/cheung/graph.zip Figure 6.14. Block diagram of the proposed GLRNet that employs a graph Laplacian regularization layer for image denoising. © 2019 IEEE. Reprinted, with permission, from Zeng et al.(2019) Figure 6.15. Block diagram of the overall DeepGLR framework. © 2019 IEEE. Reprinted, with permission, from Zeng et al.(2019) Figure 6.16. DeepAGF framework. Top: Block diagram of the AGFNet, using analytical graph filter for image denoising. Bottom: Block diagram of the N stacks DeepAGF framework. © 2020 IEEE. Reprinted, with permission, from Su et al.(2020). For a color version of this figure, see www.iste.co.uk/cheung/graph.zip Figure 6.17. Denoising result comparison on the Starfish image with input noisy level σ = 70(a) Original,(b) DnCNN(Zhang et al. 2017) and(c) DeepAGF. DnCNN and DeepAGF are trained with noise level σ = 50. © 2020 IEEE. Reprinted, with permission, from Su et al.(2020). For a color version of this figure, see www.iste.co.uk/cheung/graph.zip
Читать дальше

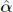 their quantized version Figure 5.6. Illustration of the difference between a compact and a not compact representation. For a color version of this figure, see www.iste.co.uk/cheung/graph.zip Figure 5.7. Graph topology for light fields and multi-view images. For a color version of this figure, see www.iste.co.uk/cheung/graph.zip Figure 5.8. Graph topology for point clouds. For a color version of this figure, see www.iste.co.uk/cheung/graph.zip Figure 5.9. Graph topology for omnidirectional images based on two different sampling approaches. For a color version of this figure, see www.iste.co.uk/cheung/graph.zip Figure 5.10. Example of a rate-distortion optimized graph partition in an omnidirectional image. Left: in the equirectangular domain; right: in the sphere domain. For a color version of this figure, see www.iste.co.uk/cheung/graph.zip Figure 5.11. Illustration of the output of the optimization process for a super-ray in four views of a light field. The first row corresponds to a super-ray across four views of the light field. The signal on the vertices corresponds to the color values lying on super-pixels corresponding to the same super-ray and the blue lines denote the correspondences based on the geometrical information in hand. The second to fourth rows are illustrations of basis functions before and after optimization. The signals on the vertices are the eigenvectors values. For a color version of this figure, see www.iste.co.uk/cheung/graph.zip
their quantized version Figure 5.6. Illustration of the difference between a compact and a not compact representation. For a color version of this figure, see www.iste.co.uk/cheung/graph.zip Figure 5.7. Graph topology for light fields and multi-view images. For a color version of this figure, see www.iste.co.uk/cheung/graph.zip Figure 5.8. Graph topology for point clouds. For a color version of this figure, see www.iste.co.uk/cheung/graph.zip Figure 5.9. Graph topology for omnidirectional images based on two different sampling approaches. For a color version of this figure, see www.iste.co.uk/cheung/graph.zip Figure 5.10. Example of a rate-distortion optimized graph partition in an omnidirectional image. Left: in the equirectangular domain; right: in the sphere domain. For a color version of this figure, see www.iste.co.uk/cheung/graph.zip Figure 5.11. Illustration of the output of the optimization process for a super-ray in four views of a light field. The first row corresponds to a super-ray across four views of the light field. The signal on the vertices corresponds to the color values lying on super-pixels corresponding to the same super-ray and the blue lines denote the correspondences based on the geometrical information in hand. The second to fourth rows are illustrations of basis functions before and after optimization. The signals on the vertices are the eigenvectors values. For a color version of this figure, see www.iste.co.uk/cheung/graph.zip










