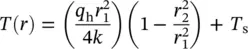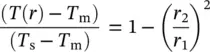(1.120) 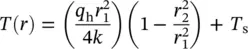
After combining terms, the dimensionless temperature equation results:
(1.121) 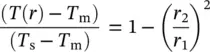
The approach mentioned previously can also be used for obtaining the temperature distributions in solid spheres and spherical shells for a wide range of boundary conditions.
Heat transfer by natural (or free) convection involving motion in a fluid is due to differences in density and the action of gravity, which causes a natural circulation flow and leads to heat transfer. For many problems involving fluid flow across a surface, the superimposed effect of natural convection is negligibly small. The heat transfer coefficients for natural convection are generally much lower than that for forced convection. When there is no forced velocity of the fluid, heat is transferred entirely by natural convection (when there is negligible radiation). For some practical cases, it is necessary to consider the radiative effect on the total heat loss or gain. Radiation heat transfer may be of the same order of magnitude as natural convection in some circumstances even at room temperatures. Hence, wall temperatures in a room can affect the comfort of occupants.
It is pointed out that in many systems, involving multimode heat transfer effects, natural convection provides the largest resistance to heat transfer, and therefore plays an important role in the design or performance of the system. Moreover, when it is desirable to minimize the heat transfer rates or to minimize operating costs, natural convection is often preferred to forced convection.
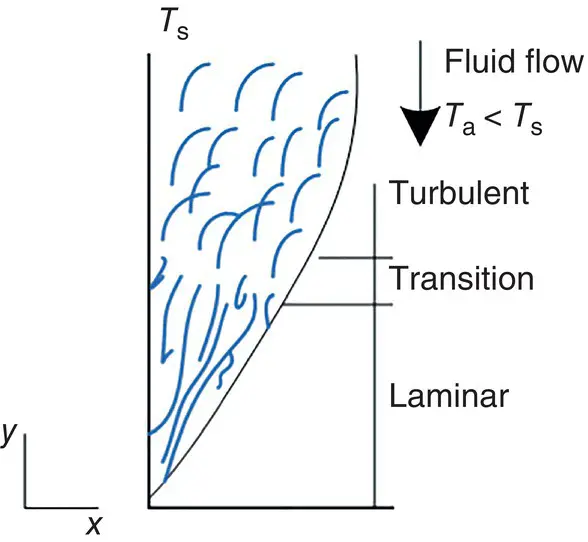
Figure 1.21 Natural convection on a vertical plate.
Natural convection is of significance in a wide variety of heating, cooling, and air‐conditioning equipments. Natural convection heat transfer is influenced mainly by the gravitational force from thermal expansion, viscous drag, and thermal diffusion. For this reason, the gravitational acceleration, the coefficient of performance, the kinematic viscosity, and the thermal diffusivity directly affect natural convection. As shown in Table 1.8, these parameters depend on the fluid properties, the temperature difference between the surface and the fluid, and the characteristic length of the surface, which are involved in the Nusselt, Grashof, and Prandtl equations.
The natural convection boundary layers are not restricted to laminar flow. In many cases, there is a transition from laminar to turbulent flow. This is schematically shown in Figure 1.21for a heated vertical plate.
Transition in a natural convection boundary layer is dependent on the relative magnitude of the buoyancy and viscous forces in the fluid. It is customary to correlate its occurrence in terms of the Rayleigh number. For example, for vertical plates the critical Rayleigh number is Ra ≈ 10 9. As in forced convection, transition to turbulence has a strong effect on the heat transfer. Numerous natural convection heat transfer correlations for several plates, pipes, wires, cylinder, and so on, along with a list of heat transfer coefficients, which were compiled from the literature, are given in Table 1.10. To calculate the natural convection heat transfer coefficient, one evaluates the Rayleigh number to determine whether the boundary layer is laminar or turbulent, and then applies the appropriate equation from this table.
The study of forced convection is concerned with the heat transfer occurring between a forced moving fluid and a solid surface. To apply Newton's law of cooling as given in Eq. (1.85), it is necessary to determine the heat transfer coefficient. For this purpose, the Nusselt–Reynolds correlations may be used. The definitions of the Nusselt and Reynolds numbers have been given in Table 1.9. Forced air and water coolers, forced air and water evaporators and condensers, and heat exchangers are examples of equipments commonly involved in forced convection heat transfer.
Table 1.10 Natural convection heat transfer equations and correlations.
Source: Olson and Wright [8].
| Equation or correlation |
| • General equations |
| Nu = hY / k f= c Ra nand Ra = Gr Pr = gβ ( T s− T a) Y 3/ νa |
| where n is 1/4 for laminar flow and 1/3 for turbulent flow. Y denotes the height for vertical plates or pipes, diameter for horizontal pipes, and radius for spheres. T fm≡ ( T s+ T a)/2. |
| • Correlations for vertical plates (or inclined plates, inclined up to 60 °) |
| Nu = [0.825 + 0.387Ra 1/6/(1 + (0.492/Pr) 9/16) 4/9] 2for an entire range of Ra |
| Nu = 0.68 + 0.67Ra 1/4/(1 + (0.492/Pr) 9/16) 4/9for 0 < Ra < 10 9 |
| • Correlations for horizontal plates ( Y ≡ A s/ P ) |
| For upper surface of heated plate or lower surface of cooled plate: |
| Nu = 0.54Ra 1/4for 10 4≤ Ra ≤ 10 7 |
| Nu = 0.15Ra 1/3for 10 7≤ Ra ≤ 10 11 |
| For lower surface of heated plate or upper surface of cooled plate: |
| Nu = 0.27Ra 1/4for 10 5≤ Ra ≤ 10 10 |
| • Correlations for horizontal cylinders |
| Nu = hD / k = c Ra n |
| where |
| c = 0.675 and n = 0.058 for 10 −10 < Ra < 10 −2 |
| c = 1.020 and n = 0.148 for 10 −2 < Ra < 10 2 |
| c = 0.850 and n = 0.188 for 10 2 < Ra < 10 4 |
| c = 0.480 and n = 0.250 for 10 4 < Ra < 10 7 |
| c = 0.125 and n = 0.333 for 10 7 < Ra < 10 12 |
| Nu = [0.60 + 0.387Ra 1/6/(1 + (0.559/Pr) 9/16) 8/27] 2for an entire range of Ra |
| • Correlations for spheres |
| Nu = 2 + 0.589Ra 1/4/(1 + (0.469/Pr) 9/16) 4/9for Pr ≥ 0.7 and Ra ≤ 10 11 |
| • Heat transfer correlations |
| Gr Pr = 1.6 × 10 6 Y 3(Δ T ) |
| with Y in m; ∆ T in °C. |
| h = 0.29(∆ T / Y ) 1/4for vertical small plates in laminar range |
| h = 0.19(∆ T ) 1/3for vertical large plates in turbulent range |
| h = 0.27(∆ T / Y ) 1/4for horizontal small plates in laminar range (facing upward when heated or downward when cooled) |
| h = 0.22(∆ T ) 1/3for vertical large plates in turbulent range (facing downward when heated or upward when cooled) |
| h = 0.27(∆ T / Y ) 1/4for small cylinders in laminar range |
| h = 0.18(∆ T ) 1/3for large cylinders in turbulent range |
The various kinds of forced convection, such as flow in a tube, flow across a tube, and flow across a flat plate, may be solved mathematically when certain assumptions are made with regard to the boundary conditions. It is extremely difficult to obtain exact solutions to such problems, especially in the event of turbulent flow, but approximate solutions can sometimes be obtained using appropriate assumptions.
Читать дальше