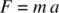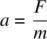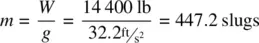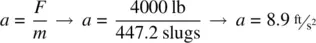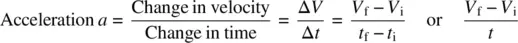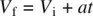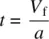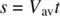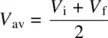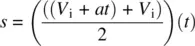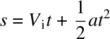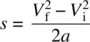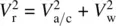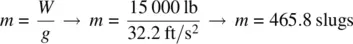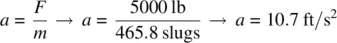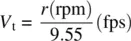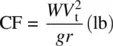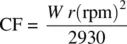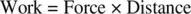Joseph R. Badick - Flight Theory and Aerodynamics

The amount of the acceleration a is directly proportional to the unbalanced force, F , and is inversely proportional to the mass, m , of the body. For a constant mass, force equals mass times acceleration.

Newton’s second law can be expressed by the simple equation:

(1.3)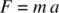

Then, solving for a ,

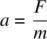
An airplane that weighs 14 400 lb accelerates down a runway with a net force of 4 000 lb, what is the acceleration ( a ) assuming constant acceleration?

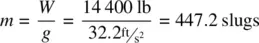
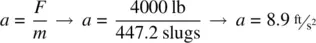
The third law states that for every action force there is an equal and opposite reaction force . Note that for this law to have any meaning, there must be an interaction between the force and a body. For example, the gases produced by burning fuel in a rocket engine are accelerated through the rocket nozzle. The equal and opposite force acts on the interior walls of the combustion chamber, and the rocket is accelerated in the opposite direction. As a propeller aircraft pushes air backward from the propeller, the aircraft is pushed forward.

Newton’s laws of motion express relationships among force, mass, and acceleration, but they stop short of discussing velocity, time, and distance. These are covered here. In the interest of simplicity, we assume here that acceleration is constant. Then,

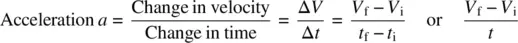
where

Δ (cap delta) means “change in”

Vf = final velocity at time tf

Vi = initial velocity at time ti

If we start the time at t i= 0 and rearrange the above, then

(1.4)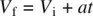

If we start the time at t i= 0 and V i= 0 (brakes locked before takeoff roll) and rearrange the above where V fcan be any velocity given, for example liftoff velocity, then

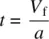
The distance s traveled in a certain time is

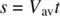
where the average velocity V avis

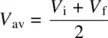
And incorporating Eq. 1.4, and substituting for V f, we get

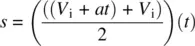
which yields

(1.5)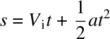

Solving Eqs. 1.4and 1.5simultaneously and eliminating t , we can derive a third equation:

(1.6)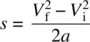

Equations 1.3– 1.6are useful in calculating takeoff and landing factors, and are studied in more detail in Chapters 8and 9.

An aircraft that weighs 15 000 lb begins from a brakes‐locked position on the runway, and then accelerates down the runway with a net force of 5000 lb until liftoff at a velocity of 110 kts. Calculate the average acceleration down the runway, the average time it takes to reach liftoff speed, and the total takeoff distance on the runway.

First, to calculate the acceleration, we need find the force ( F ) and the mass of the aircraft during the takeoff roll, Eq. 1.3: F = m a

Finding the mass:

Finding the average acceleration: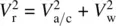

Average time to liftoff: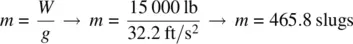

Total takeoff distance: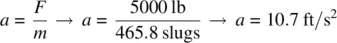

Without derivation, some of the relationships among tangential (tip) velocity, V t; radius of rotation, r ; revolutions per minute, rpm; centripetal forces, CF; weight of rotating parts, W ; and acceleration of gravity, g , are shown below. A more detailed discussion regarding rotorcraft can be found in Chapter 15of this textbook.

(1.7)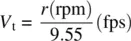

(1.8)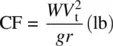

(1.9)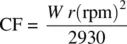

For our discussion, the units of work will be measured in ft‐lb.

Energy is the ability to do work. In physics, work has a meaning different from the popular definition. You can push against a solid wall until you are exhausted but, unless the wall moves, you are not doing any work. Work requires that a force must move an object (displacement) in the direction of the force. Another way of saying this is that only the component of the force in the direction of movement does any work:

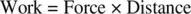
There are many kinds of energy: solar, chemical, heat, nuclear, and others. The type of energy that is of interest to us in aviation is mechanical energy .

There are two kinds of mechanical energy: The first is called potential energy of position , or more simply potential energy , PE. No movement is involved in calculating PE. A good example of this kind of energy is water stored behind a dam. If released, the water would be able to do work, such as running a generator. As a fighter aircraft zooms to a zenith point, it builds PE; once it starts to accelerate downward, it converts PE to KE. PE equals the weight, W , of an object multiplied by the height, h , of the object above some base plane: