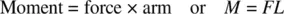Joseph R. Badick - Flight Theory and Aerodynamics

Figure 1.4 Vector of a north wind.

Figure 1.5 Vector addition.

The groundspeed is the hypotenuse of the right triangle and is found by use of the Pythagorean theorem :

The drift angle is the angle whose tangent is V w/ V a/c= 30/300 = 0.1, which is 5.7° to the right (south) of the aircraft heading.

It is often desirable to replace a given vector by two or more other vectors. This is called vector resolution . The resulting vectors are called component vectors of the original vector and, if added vectorially, they will produce the original vector. For example, if an aircraft is in a steady climb, at an airspeed of 200 kts., and the flight path makes a 30° angle with the horizontal, the groundspeed and rate of climb can be found by vector resolution. The flight path and velocity are shown by vector V a/cin Figure 1.6.

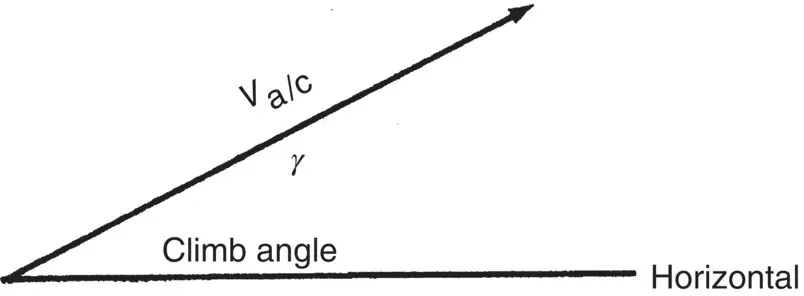
Figure 1.6 Vector of an aircraft in a climb.

Figure 1.7 Vectors of groundspeed and rate of climb.

In Figure 1.7, to resolve the vector V a/cinto a component V hparallel to the horizontal, which will represent the groundspeed, and a vertical component, V v, which will represent the rate of climb, we simply draw a straight line vertically upward from the horizontal to the tip of the arrow V a/c. This vertical line represents the rate of climb and the horizontal line represents the groundspeed of the aircraft. If the airspeed V a/cis 200 kts. and the climb angle is 30°, mathematically the values are

If a mechanic tightens a nut by applying a force to a wrench, a twisting action, called a moment , is created about the center of the bolt. This particular type of moment is called torque (pronounced “tork”). Moments, M , are measured by multiplying the amount of the applied force, F , by the moment arm , L :

(1.2)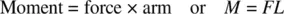

The moment arm is the perpendicular distance from the line of action of the applied force to the center of rotation. Moments are measured as foot–pounds (ft‐lb) or as inch–pounds (in.‐lb). If a mechanic uses a 10 in.‐long wrench and applies 25 lb of force, the torque on the nut is 250 in.‐lb.

The aircraft moments that are of particular interest to pilots include pitching moments, yawing moments, and rolling moments. If you have ever completed a weight and balance computation for an aircraft, you have calculated a moment, where weight was the force and the arm was the inches from datum. Pitching moments, for example, occur when an aircraft’s elevator is moved. Air loads on the elevator, multiplied by the distance to the aircraft’s center of gravity (CG), create pitching moments, which cause the nose to pitch up or down. As you can see from Eq. 1.2, if a force remains the same but the arm is increased, the moment increases.

Several forces may act on an aircraft at the same time, and each will produce its own moment about the aircraft’s CG. Some of these moments may oppose others in direction. It is therefore necessary to classify each moment, not only by its magnitude, but also by its direction of rotation. One such classification could be by clockwise or counterclockwise rotation. In the case of pitching moments, a nose‐up or nose‐down classification seems appropriate.

Mathematically, it is desirable that moments be classified as positive (+) or negative (−). For example, if a clockwise moment is considered to be a + moment, then a counterclockwise moment must be considered to be a − moment. By definition, aircraft nose‐up pitching moments are considered to be + moments.

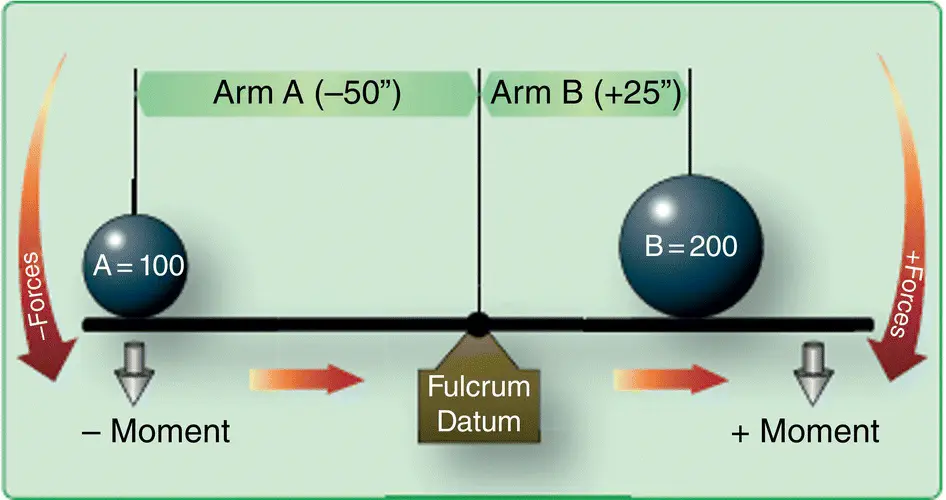
Figure 1.8 Balance Lever.

Webster defines equilibrium as “a state in which opposing forces or actions are balanced so that one is not stronger or greater than the other.” A body must meet two requirements to be in a state of equilibrium:

1 There must be no unbalanced forces acting on the body. This is written as the mathematical formula ∑F = 0, where ∑ (cap sigma) is the Greek symbol for “sum of.” Figure 1.2illustrates the situation where this condition is satisfied (lift = weight, thrust = drag, etc.)

2 There must be no unbalanced moments acting on the body. Mathematically, ∑M = 0.Moments at the fulcrum in Fig. 1.8are 5000 ft‐lb clockwise and 5000 ft‐lb counterclockwise. The weight (force) of A is 100 lb and is located 50 inches (″) to the left of datum (fulcrum), thus 100 lb × −50″ = −5000 lb‐in. The weight of B is 200 lb and is located 25 inches to the right of datum, thus 200 lb × 25″ = 5000 lb‐in. So, ∑M = 0.

Sir Isaac Newton summarized three generalizations about force and motion. These are known as the laws of motion .

In simple language, the first law states that a body at rest will remain at rest and a body in motion will remain in motion, in a straight line, unless acted upon by an unbalanced force . The first law implies that bodies have a property called inertia . Inertia may be defined as the property of a body that results in its maintaining its velocity unchanged unless it interacts with an unbalanced force. For example, an aircraft parked on the ramp would not even need chocks unless an unbalanced force (such as wind, or gravity if parked on a slope) acted on it. The measure of inertia is what is technically known as mass .

The second law states that if a body is acted on by an unbalanced force, the body will accelerate in the direction of the force and the acceleration will be directly proportional to the force and inversely proportional to the mass of the body. Acceleration is the change in the velocity of a body in a unit of time. Consider an aircraft accelerating down the runway, or decelerating after touchdown. For our discussion, the primary forces acting on an aircraft accelerating or decelerating down a runway are thrust, drag, and friction. Future chapters will discuss the net force on an aircraft during the takeoff and landing regimes.