p -1 Factoring Algorithm 19.9 Latin Squares 19.10 Computational Complexity, Turing Machines, Quantum Computing 19.11 Problems 19.12 Solutions Note Chapter 20: Introduction to Linear Codes 20.1 Repetition Codes and Parity Checks 20.2 Details of Linear Codes 20.3 Parity Checks, the Syndrome, and Weights 20.4 Hamming Codes, an Inequality 20.5 Perfect Codes, Errors, and the BSC 20.6 Generalizations of Binary Hamming Codes 20.7 The Football Pools Problem, Extended Hamming Codes 20.8 Golay Codes 20.9 McEliece Cryptosystem 20.10 Historical Remarks 20.11 Problems 20.12 Solutions Chapter 21: Cyclic Linear Codes, Shift Registers, and CRC 21.1 Cyclic Linear Codes 21.2 Generators for Cyclic Codes 21.3 The Dual Code 21.4 Linear Feedback Shift Registers and Codes 21.5 Finding the Period of a LFSR 21.6 Cyclic Redundancy Check (CRC) 21.7 Problems 21.8 Solutions Chapter 22: Reed‐Solomon and MDS Codes, and the Main Linear Coding Theory Problem (LCTP) 22.1 Cyclic Linear Codes and Vandermonde 22.2 The Singleton Bound for Linear Codes 22.3 Reed–Solomon Codes 22.4 Reed‐Solomon Codes and the Fourier Transform Approach 22.5 Correcting Burst Errors, Interleaving 22.6 Decoding Reed‐Solomon Codes, Ramanujan, and Berlekamp–Massey 22.7 An Algorithm for Decoding and an Example 22.8 Long MDS Codes and a Partial Solution of a 60 Year‐Old Problem 22.9 Problems 22.10 Solutions Chapter 23: MDS Codes, Secret Sharing, and Invariant Theory 23.1 Some Facts Concerning MDS Codes 23.2 The Case
k = 2 , Bruck Nets 23.3 Upper Bounds on MDS Codes, Bruck–Ryser 23.4 MDS Codes and Secret Sharing Schemes 23.5 MacWilliams Identities, Invariant Theory 23.6 Codes, Planes, and Blocking Sets 23.7 Long Binary Linear Codes of Minimum Weight at Least 4 23.8 An Inverse Problem and a Basic Question in Linear Algebra Chapter 24: Key Reconciliation, Linear Codes, and New Algorithms 24.1 Symmetric and Public Key Cryptography 24.2 General Background 24.3 The Secret Key and the Reconciliation Algorithm 24.4 Equality of Remnant Keys: The Halting Criterion 24.5 Linear Codes: The Checking Hash Function 24.6 Convergence and Length of Keys 24.7 Main Results 24.8 Some Details on the Random Permutation 24.9 The Case Where Eve Has Nonzero Initial Information 24.10 Hash Functions Using Block Designs 24.11 Concluding Remarks Note Chapter 25: New Identities for the Shannon Function with Applications 25.1 Extensions of a Binary Symmetric Channel 25.2 A Basic Entropy Equality 25.3 The New Identities 25.4 Applications to Cryptography and a Shannon‐Type Limit 25.5 Problems 25.6 Solutions Chapter 26: Blockchain and Bitcoin 26.1 Ledgers, Blockchains 26.2 Hash Functions, Cryptographic Hashes 26.3 Digital Signatures 26.4 Bitcoin and Cryptocurrencies 26.5 The Append‐Only Network, Identities, Timestamp, Definition of a Bitcoin 26.6 The Bitcoin Blockchain and Merkle Roots 26.7 Mining, Proof‐of‐Work, Consensus 26.8 Thwarting Double Spending Chapter 27: IoT, The Internet of Things 27.1 Introduction 27.2 Analog to Digital (A/D) Converters 27.3 Programmable Logic Controller 27.4 Embedded Operating Systems 27.5 Evolution, From SCADA to the Internet of Things 27.6 Everything is Fun and Games until Somebody Releases a Stuxnet 27.7 Securing the IoT, a Mammoth Task 27.8 Privacy and Security Notes Chapter 28: In the Cloud 28.1 Introduction 28.2 Distributed Systems 28.3 Cloud Storage – Availability and Copyset Replication 28.4 Homomorphic Encryption 28.5 Cybersecurity 28.6 Problems 28.7 Solutions Chapter 29: Review Problems and Solutions29.1 Problems 29.2 Solutions
13 Appendix AA.1 ASCII
14 Appendix BB.1 Shannon's Entropy Table
15 Glossary
16 References
17 Index
18 End User License Agreement
1 Chapter 2 Table 2.1 Approximate frequencies of letters in the English language. Table 2.2 Number of character coincidences corresponding to displacement
2 Chapter 21Table 21.1 Factorization of 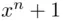 over
over 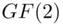
3 Chapter 24Table 24.1 Bit agreements between two remnant stringsTable 24.2 Expressions for 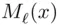 for
for 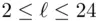 Table 24.3 Expressions for
Table 24.3 Expressions for 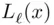 for
for 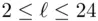 Table 24.4 Optimal values for
Table 24.4 Optimal values for 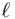 Table 24.5 Reconciling two 400 bit keys
Table 24.5 Reconciling two 400 bit keys
4 Appendix ATable A.1 ASCII table
5 Appendix BTable B.1 Shannon's entropy table.
1 Chapter 1 Figure 1.1 (a) Claude E. Shannon, Theseus, and the maze (see Section 1.4). (...
2 Chapter 2 Figure 2.1 Caesar cipher wheel. Figure 2.2 The German Enigma machine. (a) the Enigma machine type‐K, (b) the... Figure 2.3 Block diagram of the Enigma machine. Figure 2.4 Simplified Enigma model.
3 Chapter 3 Figure 3.1 General encryption. Figure 3.2 Symmetric encryption. Figure 3.3 Asymmetric or public encryption.
4 Chapter 4 Figure 4.1 One‐time pad. Figure 4.2 How does Romeo know that Juliet's message has not been altered? Figure 4.3 Authentication and message integrity check to ensure that nobody ... Figure 4.4 Public key encryption principle. Figure 4.5 Digital signature scheme usingPublic Key Cryptography.Figure 4.6 The basic Kerberos scheme for trusted server authentication.
5 Chapter 6Figure 6.1 The group law.
6 Chapter 7Figure 7.1 Man‐in‐the‐middle attack on symmetric key encryption.Figure 7.2 Man‐in‐the‐middle attack on public key encryption.Figure 7.3 A passive relay attack in which encrypted message 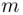 is sent by Al...Figure 7.4 A relay attack. Message
is sent by Al...Figure 7.4 A relay attack. Message 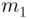 is sent by Alice's car. Everelays (for...
is sent by Alice's car. Everelays (for...
7 Chapter 11Figure 11.1: Decision tree.Figure 11.2: Initial graph.Figure 11.3: After one merge.Figure 11.4: Arithmetic coding.
8 Chapter 13Figure 13.1: The German 10 Deutsche Mark featured Gauss in the 1990s.Figure 13.2: The late Professor J. H. van Lint, one of the world's leading c...
9 Chapter 16Figure 16.1: One clock pulse.Figure 16.2: A general LFSR.Figure 16.3: The 5‐bit LFSR generated by 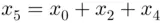 .
.
10 Chapter 17Figure 17.1 Memory hierarchy.Figure 17.2 Memory hierarchy with compressed caching included.Figure 17.3 Compressed caching in main memory.Figure 17.4 Lempel–Ziv tree for the string 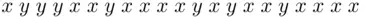 .Figure 17.5 Dictionary immediately after compressing
.Figure 17.5 Dictionary immediately after compressing 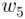 in Example 17.5. Afte...Figure 17.6 Cells 1 (top), 2 (middle), and 3 (bottom) in the compressed cach...Figure 17.7 Cell 2 after adding a compressed page
in Example 17.5. Afte...Figure 17.6 Cells 1 (top), 2 (middle), and 3 (bottom) in the compressed cach...Figure 17.7 Cell 2 after adding a compressed page 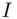 of size 0.7.Figure 17.8 Cells 1 (top), 2 (middle), and 3 (bottom) for Problem 17.5.Figure 17.9 Cell 1 for Solution 17.5.
of size 0.7.Figure 17.8 Cells 1 (top), 2 (middle), and 3 (bottom) for Problem 17.5.Figure 17.9 Cell 1 for Solution 17.5.
Читать дальше

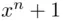 over
over 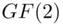
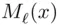 for
for 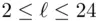 Table 24.3 Expressions for
Table 24.3 Expressions for 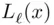 for
for 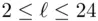 Table 24.4 Optimal values for
Table 24.4 Optimal values for 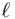 Table 24.5 Reconciling two 400 bit keys
Table 24.5 Reconciling two 400 bit keys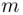 is sent by Al...Figure 7.4 A relay attack. Message
is sent by Al...Figure 7.4 A relay attack. Message 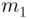 is sent by Alice's car. Everelays (for...
is sent by Alice's car. Everelays (for...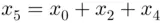 .
.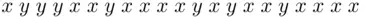 .Figure 17.5 Dictionary immediately after compressing
.Figure 17.5 Dictionary immediately after compressing 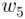 in Example 17.5. Afte...Figure 17.6 Cells 1 (top), 2 (middle), and 3 (bottom) in the compressed cach...Figure 17.7 Cell 2 after adding a compressed page
in Example 17.5. Afte...Figure 17.6 Cells 1 (top), 2 (middle), and 3 (bottom) in the compressed cach...Figure 17.7 Cell 2 after adding a compressed page 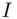 of size 0.7.Figure 17.8 Cells 1 (top), 2 (middle), and 3 (bottom) for Problem 17.5.Figure 17.9 Cell 1 for Solution 17.5.
of size 0.7.Figure 17.8 Cells 1 (top), 2 (middle), and 3 (bottom) for Problem 17.5.Figure 17.9 Cell 1 for Solution 17.5.










