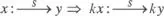Al finalizar el presente capítulo el lector será capaz de:
Distinguir los diferentes elementos circuitales activos y pasivos.
Reconocer de un subsistema su comportamiento como fuente de tensión o como fuente de corriente.
Profundizar en el conocimiento de resistores, inductores y condensadores.
Aplicar correctamente las leyes fundamentales de la electricidad.
Analizar regímenes transitorios en circuitos de primer y segundo orden.
Resolver gráficamente un circuito mediante su recta de carga.
Operar tanto en el dominio temporal como en el dominio de la frecuencia, utilizando series de Fourier y su cálculo discreto mediante la transformada rápida de Fourier.
2.1. Definiciones previas
En este apartado se expondrán unas cuantas definiciones y relaciones básicas entre magnitudes eléctricas que serán utilizadas a lo largo de la obra.
En este texto se seguirán los siguientes convenios generales para representar magnitudes:
En mayúsculas se representarán magnitudes o valores constantes. Cuando convenga se utilizarán subíndices para remarcar alguna propiedad sobre un determinado valor. Por ejemplo E o Imed.
En minúsculas se representarán magnitudes genéricas que pueden depender del tiempo (e, i). Esta propiedad se remarcará específicamente cuando así convenga. Por ejemplo, u(t) o w(t).
Para tensiones y corrientes impuestas por fuentes se utilizarán las designaciones e y j respectivamente, mientras que para magnitudes derivadas se utilizarán u y v para tensiones e i para corrientes.
Se utilizará el Sistema Internacional (S.I.) de unidades.
2.1.1. Magnitudes de interés
Carga eléctrica q:
Propiedad intrínseca de la materia.
Unidad: Coulomb (C)
1 C= 6,24 10 18electrones (1e = 1,602 10 -19C)
Intensidad de corriente eléctrica i:Flujo de carga eléctrica por unidad de tiempo.

Unidad: Ampère (A)
1 A =1 C/1 s
Carga transferida en el intervalo [ t0-t ]:

Energía w:
Capacidad de realizar un trabajo. Dicha capacidad depende de la existencia de alguna fuerza, por lo que en función del tipo de fuerza existirán diversas formas de energía: cinética, potencial, térmica, gravitacional, electromagnética, etc. En el caso de la energía eléctrica, esta se debe a la presencia de cargas sometidas a una diferencia de potencial.

Como de (2.1), dq(t) = i(t) dt resulta que otra expresión para la energía eléctrica es

Unidad: Joule (J)
1 J= 1 W·1 s(trabajo realizado por 1 W durante 1 s)
3 600 J= 1 W·1 h= 1 Wh
3 600 000 J= 1 kWh
Potencia p:
Cantidad de trabajo efectuado por unidad de tiempo.

Unidad: Watt (W)
1 W= 1 J/1 s
Tensión, voltaje o diferencia de potencial u:
Energía necesaria para mover la unidad de carga.

Unidad: Volt ( V)
1 V= 1 J/1 C
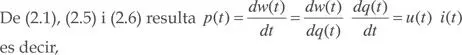

La energía que absorbe o suministra un elemento en el intervalo [ t 0- t ], de acuerdo con (2.5) y (2.7), es
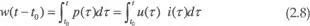
Flujo magnético Φ:
Medida de la cantidad de magnetismo. En presencia de un campo magnético se relaciona con la diferencia de potencial según:

Unidad: Weber (Wb)
1 V= 1 Wb/1 s
2.1.2. Algunas definiciones
En el primer capítulo de este libro se han utilizado repetidamente los términos sistemay señal.Resulta obligado definirlos:
Sistema
Se denomina sistemaa la asociación de dos conjuntos ordenados. Uno de c omponentes,{C j}, y otro de enlaces,{E k},

Estos dos conjuntos permiten el conocimiento de la estructurade dicho sistema.
Si conociendo la estructura y la entrada de un sistema se obtiene la respuesta, se dice que se ha realizado su análisis.Si conociendo la entrada y la salida de un sistema se determina su estructura, se realiza su síntesis.
Si se conoce la salida del sistema para cualquier entrada se dice que se conoce el comportamientode dicho sistema.
Linealidad
Sea un sistema, S , de entrada x y salida y :
Si 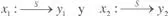 Se dice que el sistema es linealsi y sólo si
Se dice que el sistema es linealsi y sólo si 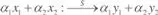 . Es decir, que un sistema es lineal si y sólo si una combinación lineal de las entradas origina, como respuesta, la misma combinación lineal de las respuestas obtenidas cuando las entradas se aplican individualmente al sistema.
. Es decir, que un sistema es lineal si y sólo si una combinación lineal de las entradas origina, como respuesta, la misma combinación lineal de las respuestas obtenidas cuando las entradas se aplican individualmente al sistema.
Un sistema lineal, por tanto, cumple con:
la homogeneidad (proporcionalidad), ya que:
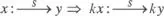
y la aditividad, ya que:
Читать дальше







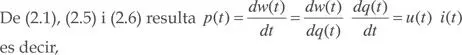

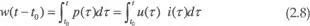


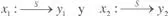 Se dice que el sistema es linealsi y sólo si
Se dice que el sistema es linealsi y sólo si 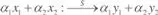 . Es decir, que un sistema es lineal si y sólo si una combinación lineal de las entradas origina, como respuesta, la misma combinación lineal de las respuestas obtenidas cuando las entradas se aplican individualmente al sistema.
. Es decir, que un sistema es lineal si y sólo si una combinación lineal de las entradas origina, como respuesta, la misma combinación lineal de las respuestas obtenidas cuando las entradas se aplican individualmente al sistema.