Diagnosis and Fault-tolerant Control 1

A conventional feedback control design for complex systems may result in unsatisfactory performance in the event of malfunction in input–output sensors, actuators and system components. A fault-tolerant closed-loop control system is very attractive because it can tolerate faults while also maintaining desirable performance.

The conventional approach to the design of an FTC includes different steps and separate modules: modeling or identification of the controlled system, design of the controller, FDI scheme and a method for re-configuring the control system. Identification and design of the controller can be performed separately or using combined methods. Hence, the FDI and controller are linked through the reconfiguration module. The fundamental problem with such a system lies in the identification stage in the independent design of the control and FDI modules. Significant interactions occurring among these modules can be neglected. There is therefore a need for a research study into the interactions between system identification, control design, the FDI stage and the FTC design strategy.

Fault identification is the most important of all the fault diagnosis tasks. When a fault is estimated, detection and isolation can be easily achieved since the fault nature can improve the diagnosis process. However, the fault identification problem itself has not gained enough research attention.

Most fault diagnosis techniques, such as parameter identification, parity space and observer-based methods, cannot be directly used to identify faults in sensors and actuators. Very little research has been done to overcome the fault identification problem. The Kalman filter for statistical testing and fault identification was proposed in Chen and Patton (1999). However, the statistical testing methods can impose a high computational demand. A fault identification scheme solving a system inversion problem was proposed in Chen and Patton (1999); Simani et al . (2003) and Simani and Farsoni (2018).

In the scheme, depicted in Figure I.3, fault identification is performed by estimating the nonlinear relationship between residuals and fault magnitudes. This is possible because robust residuals should only contain fault information.

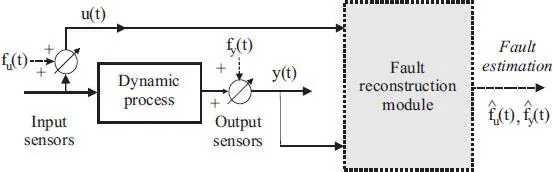
Figure I.3. Fault estimation scheme FTC

Such a nonlinear function approximation and estimation can be performed by using fuzzy systems, neural networks or an inversion of the transfer matrix between residuals and faults (Simani et al . 2003; Simani and Farsoni 2018). The central task in model-based fault detection is the residual generation. Most residual generation techniques are based on linear system models. For nonlinear systems, the traditional approach is to linearize the model around the system operating point. However, for systems with high nonlinearity and a wide dynamic operating range, the linearized approach fails to give satisfactory results.

One solution is to use a large number of linearized models corresponding to a range of operating points. This means that a large number of FDI schemes corresponding to each of the operating points is needed. Hence, it is important to study residual generation techniques that tackle nonlinear dynamic systems directly. There are some research studies on the residual generation of nonlinear dynamic systems, for example using nonlinear observers (Chen and Patton 1999; De Persis and Isidori 2001). There have been some attempts to use nonlinear observers to solve nonlinear system FDI problems, (Chen and Patton 1999; De Persis and Isidori 2001), for example, nonlinear UIOs, including adaptive observers and sliding mode observers. If the class of nonlinearities can be restricted, observers for bilinear systems were also proposed (Chen and Patton 1999).

On the other hand, the analytical models that the nonlinear observer approaches are based on are not easy to obtain in practice. Sometimes, it is impossible to model the system using an explicit mathematical model. To overcome this problem, it is desirable to find a universal approximate model that can be used to represent the real system with an arbitrary degree of accuracy. Different approaches were proposed and they are currently under investigation: neural networks, fuzzy models and hybrid models.

As shown in Simani et al . (2003) and Simani and Farsoni (2018), fuzzy systems and neural networks are a powerful tool for handling nonlinear problems. One of the most important advantages of neural networks is their ability to implement nonlinear transformations for functional approximation problems. Therefore, neural networks can be used in a number of ways to tackle fault diagnosis problems for nonlinear dynamic systems. In existing publications, they were mainly exploited as fault classifier with steady-state processes, whereas neural networks have been used as residual generators and for modeling nonlinear dynamic systems for FDI purposes (Chen and Patton 1999).

Fuzzy models can be used both as a residual classifier and as a nonlinear system parametric model (Chen and Patton 1999). In the second case, the main idea is to build an FDI scheme based on fuzzy observers. Estimated outputs and residuals are computed as fuzzy fusion of local observer output and residuals. The main problem of this approach concerns the stability of the global observer. A linear matrix inequality method was proposed in Chen and Patton (1999) using Lyapunov theorem, but this solution can be quite conservative.

Hybrid models can describe the behavior of any nonlinear dynamic process if they are described as a composition of several local affine models, selected according to the process operating conditions (Chen and Patton 1999; Simani et al . 2003). Instead of exploiting complicated nonlinear models obtained by modeling techniques, it is possible to describe the plant by a collection of affine models. Such a compound system requires the identification of the local models from data. Several works (Chen and Patton 1999; Simani et al . 2003) addressed a method for the identification and the optimal selection of the local affine models from a sequence of noisy measurements acquired from the process. Application of these results to model-based fault diagnosis for safety critical systems is another research area worthy of mention.

To detect and isolate faults in a dynamic system, based on the use of an analytical model, a residual signal has to be used. It is derived from a comparison between real measurements and the relative estimates (generated by the model). The modeling uncertainty problem can be tackled by designing FDI and FTC schemes, whose residuals are insensitive to uncertainties while sensitive to faults. On the other hand, a model with satisfactory accuracy can be estimated using identification procedures (Norton 1986; Söderström and Stoica 1987; Ljung 1999).

The aim of the design of FDI and FTC schemes is to reduce the effects of uncertainties on the residuals and to enhance the effects of faults acting on the residuals. The main aim of this book is to develop a residual generator for model-based fault diagnosis and to design an effective FTC strategy for a dynamic process by means of input and output signals. An accurate model of the process under investigation will be estimated using identification procedures from data affected by noises and acquired from simulated and/or actual plants. The book consists of an Introduction and six chapters in Volume 1 and eight chapters in Volume 2 and the main contributions are summarized in the following.

The Introduction, provides a brief overview and critical discussion of the state of the art of the most recent literature from 2015 to 2020, thereby introducing the field of fault detection, fault diagnosis and fault-tolerant systems with methods, which have proven their significance in practical applications.