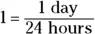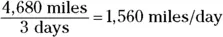Radiating heat is just one of the three ways heat can be transferred. You can discover plenty more about heat, whether created by a heat source like the sun or by friction, through the topics in Part 4.
Chapter 2
Reviewing Physics Measurement and Math Fundamentals
IN THIS CHAPTER
 Mastering measurements (and keeping them straight as you solve equations)
Mastering measurements (and keeping them straight as you solve equations)
 Accounting for significant digits and possible errors
Accounting for significant digits and possible errors
 Brushing up on basic algebra and trig concepts
Brushing up on basic algebra and trig concepts
Physics uses observations and measurements to make mental and mathematical models that explain how the world (and everything in it) works. This process is unfamiliar to most people, which is where this chapter comes in.
This chapter covers some basic skills you need for the coming chapters. We cover measurements and scientific notation, give you a refresher on basic algebra and trigonometry, and show you which digits in a number to pay attention to — and which ones to ignore. Continue on to build a physics foundation, solid and unshakable, that you can rely on throughout this book.
Measuring the World around You and Making Predictions
Physics excels at measuring and predicting the physical world — after all, that’s why physics exists. Measuring is the starting point — part of observing the world so you can then model and predict it. You have several different measuring sticks at your disposal: some for length, some for mass or weight, some for time, and so on. Mastering those measurements is part of mastering physics.
Using systems of measurement
To keep like measurements together, physicists and mathematicians have grouped them into measurement systems. The most common measurement system you see in introductory physics is the meter-kilogram-second (MKS) system, referred to as SI (short for Système International d’Unités, the International System of Units), but you may also come across the foot-pound-second (FPS) system. Table 2-1lists the primary units of measurement in the MKS system, along with their abbreviations.
TABLE 2-1Units of Measurement in the MKS System
| Measurement |
Unit |
Abbreviation |
| Length |
meter |
m |
| Mass |
kilogram |
kg |
| Time |
second |
s |
| Force |
newton |
N |
| Energy |
joule |
J |
| Pressure |
pascal |
Pa |
| Electric current |
ampere |
A |
| Magnetic flux density |
tesla |
T |
| Electric charge |
coulomb |
C |
 Because different measurement systems use different standard lengths, you can get several different numbers for one part of a problem, depending on the measurement you use. For example, if you’re measuring the depth of the water in a swimming pool, you can use the MKS measurement system, which gives you an answer in meters, or the less common FPS system, in which case you determine the depth of the water in feet. The point? When working with equations, stick with the same measurement system all the way through the problem. If you don’t, your answer will be a meaningless hodgepodge, because you’re switching measuring sticks for multiple items as you try to arrive at a single answer. Mixing up the measurements causes problems — imagine baking a cake where the recipe calls for 2 cups of flour, but you use 2 liters instead.
Because different measurement systems use different standard lengths, you can get several different numbers for one part of a problem, depending on the measurement you use. For example, if you’re measuring the depth of the water in a swimming pool, you can use the MKS measurement system, which gives you an answer in meters, or the less common FPS system, in which case you determine the depth of the water in feet. The point? When working with equations, stick with the same measurement system all the way through the problem. If you don’t, your answer will be a meaningless hodgepodge, because you’re switching measuring sticks for multiple items as you try to arrive at a single answer. Mixing up the measurements causes problems — imagine baking a cake where the recipe calls for 2 cups of flour, but you use 2 liters instead.
From meters to inches and back again: Converting between units
Physicists use various measurement systems to record numbers from their observations. But what happens when you have to convert between those systems? Physics problems sometimes try to trip you up here, giving you the data you need in mixed units: centimeters for this measurement but meters for that measurement — and maybe even mixing in inches as well. Don’t be fooled. You have to convert everything to the same measurement system before you can proceed. How do you convert in the easiest possible way? You use conversion factors, which we explain in this section.
 To convert between measurements in different measuring systems, you can multiply by a conversion factor. A conversion factor is a ratio that, when you multiply it by the item you’re converting, cancels out the units you don’t want and leaves those that you do. The conversion factor must equal 1.
To convert between measurements in different measuring systems, you can multiply by a conversion factor. A conversion factor is a ratio that, when you multiply it by the item you’re converting, cancels out the units you don’t want and leaves those that you do. The conversion factor must equal 1.
Here’s how it works: For every relation between units — for example, 24 hours = 1 day — you can make a fraction that has the value of 1. If, for example, you divide both sides of the equation 24 hours = 1 day by 1 day, you get
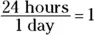
Suppose you want to convert 3 days to hours. You can just multiply your time by the preceding fraction. Doing so doesn’t change the value of the time because you’re multiplying by 1. You can see that the unit of days cancels out, leaving you with a number of hours:
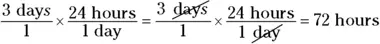
 Words such as days, seconds, and meters act like the variables x and y in that if they’re present in both the numerator and the denominator, they cancel each other out.
Words such as days, seconds, and meters act like the variables x and y in that if they’re present in both the numerator and the denominator, they cancel each other out.
To convert the other way — hours into days, in this example — you simply use the same original relation, 24 hours = 1 day, but this time divide both sides by 24 hours to get
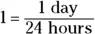
Then multiply by this fraction to cancel the units from the bottom, which leaves you with the units on the top.
Consider the following problem. Passing the state line, you note that you’ve gone 4,680 miles in exactly three days. Very impressive. If you went at a constant speed, how fast were you going? Speed is just as you may expect — distance divided by time. So you calculate your speed as follows:
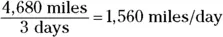
Your answer, however, isn’t exactly in a standard unit of measure. You have a result in miles per day, which you write as miles/day. To calculate miles per hour, you need a conversion factor that knocks days out of the denominator and leaves hours in its place, so you multiply by days / hour and cancel out days:
Читать дальше

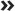 Mastering measurements (and keeping them straight as you solve equations)
Mastering measurements (and keeping them straight as you solve equations) Because different measurement systems use different standard lengths, you can get several different numbers for one part of a problem, depending on the measurement you use. For example, if you’re measuring the depth of the water in a swimming pool, you can use the MKS measurement system, which gives you an answer in meters, or the less common FPS system, in which case you determine the depth of the water in feet. The point? When working with equations, stick with the same measurement system all the way through the problem. If you don’t, your answer will be a meaningless hodgepodge, because you’re switching measuring sticks for multiple items as you try to arrive at a single answer. Mixing up the measurements causes problems — imagine baking a cake where the recipe calls for 2 cups of flour, but you use 2 liters instead.
Because different measurement systems use different standard lengths, you can get several different numbers for one part of a problem, depending on the measurement you use. For example, if you’re measuring the depth of the water in a swimming pool, you can use the MKS measurement system, which gives you an answer in meters, or the less common FPS system, in which case you determine the depth of the water in feet. The point? When working with equations, stick with the same measurement system all the way through the problem. If you don’t, your answer will be a meaningless hodgepodge, because you’re switching measuring sticks for multiple items as you try to arrive at a single answer. Mixing up the measurements causes problems — imagine baking a cake where the recipe calls for 2 cups of flour, but you use 2 liters instead. To convert between measurements in different measuring systems, you can multiply by a conversion factor. A conversion factor is a ratio that, when you multiply it by the item you’re converting, cancels out the units you don’t want and leaves those that you do. The conversion factor must equal 1.
To convert between measurements in different measuring systems, you can multiply by a conversion factor. A conversion factor is a ratio that, when you multiply it by the item you’re converting, cancels out the units you don’t want and leaves those that you do. The conversion factor must equal 1.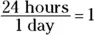
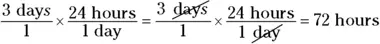
 Words such as days, seconds, and meters act like the variables x and y in that if they’re present in both the numerator and the denominator, they cancel each other out.
Words such as days, seconds, and meters act like the variables x and y in that if they’re present in both the numerator and the denominator, they cancel each other out.