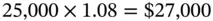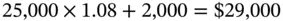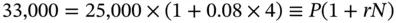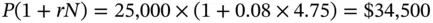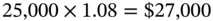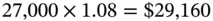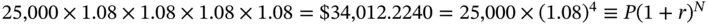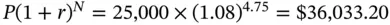Variables and Corresponding Symbols
P ≡ amount of principal that is invested at the outset
N ≡ number of measurement periods for which the investment is being made
r ≡ nominal rate of interest per measurement period
i ≡ effective rate of interest per measurement period
m ≡ number of interest conversion periods per measurement period
Take the case of an investor who makes an investment of $ P for N periods. If interest is paid on a simple basis, then we can state the following.
The interest that will be earned every period is a constant.
In every period interest is computed and credited only on the original principal.
No interest is payable on any interest that has been accumulated at an intermediate stage.
Let r be the quoted rate of interest per measurement period. Consider an investment of $ P . It will grow to $ P (1 + r ) after one period. In the second period, if simple interest is being paid, then interest will be paid only on P and not on P (1 + r ). Consequently, the accumulated value after two periods will be $ P (1 + 2 r ). In general, if the investment is made for N periods, the terminal value of the original investment will be $ P (1 + rN ). N need not be an integer, that is, investments may be made for fractional periods.
Katherine Mitchell has deposited $25,000 with Continental Bank for a period of four years. The bank pays interest at the rate of 8% per annum on a simple basis.
The growth of Katherine's deposit may be viewed as follows. An investment of $25,000 will become
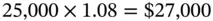
after one year. Thus, the interest for the year is $2,000. At the end of the second year, interest for the year will be paid only on the original principal of $25,000, and not on the previous year's terminal value of $27,000. Consequently, the accumulated value after two years will be
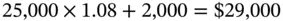
Extending the logic, the terminal balance after three years will be $31,000, and the final balance after four years will be $33,000.
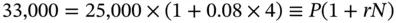
Notice the following.
The interest paid every year is a constant amount of $2,000.
Every year interest is paid only on the original deposit of $25,000.
No interest is paid on interest that is accumulated at an earlier stage.
Alex Gunning deposited $25,000 with International Bank for four years and nine months and wants to withdraw the balance at maturity. The bank pays 8% interest per annum on a simple interest basis. The terminal value in this case is given by:
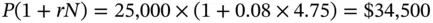
Notice that N , in this case 4.75 years, need not be an integer.
Let us take the case of an investment of $ P that has been made for N measurement periods. However, we will assume this time that interest is compounded at the end of every year. Notice, we are assuming that the interest conversion period is equal to the measurement period, namely a year. In other words, the quoted rate is equal to the effective rate.
In this case, an original investment of $ P will become $ P (1 + r ) dollars after one period. The difference as compared to the earlier case, however, is that during the second period the entire amount will earn interest and consequently the balance at the end of two periods will be P (1 + r ) 2. Extending the logic the balance after N periods will be P (1 + r ) N. Once again you should note that N need not be an integer.
Thus, the following observations are valid if interest is paid on a compound interest basis.
Every time interest is earned it is automatically reinvested at the same rate for the next conversion period.
Interest is paid on the accumulated value at the start of the conversion period and not on the original principal.
The interest earned every period will not be a constant but will steadily increase.
Assume that Katherine Mitchell has deposited $25,000 with Continental Bank for four years, and that the bank pays 8% interest per annum compounded annually.
The initial investment of $25,000 will become
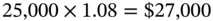
after one year. The difference in this case, as opposed to the earlier example (2.2)where simple interest was considered, is that the entire accumulated value of $27,000 will earn interest during the second year. Thus, the accumulated value after two years will be
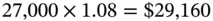
By the same logic the balance after four years will be
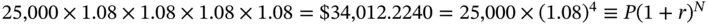
The growth pattern is illustrated in the following table.
Notice the following. In the case of simple interest, the interest paid every year was a constant amount of $2,000. In the case of compound interest, however, the amount is steadily increasing, as can be seen in the last column of Table 2.1.
TABLE 2.1The Compounding Process
| Year |
Balance at Beginning of Year |
Balance at End of Year |
Interest for Year |
| 1 |
25,000.00 |
27,000.00 |
2,000.00 |
| 2 |
27,000.00 |
29,160.00 |
2,160.00 |
| 3 |
29,160.00 |
31,492.80 |
2,332.80 |
| 4 |
31492.80 |
34,012.22 |
2,519.42 |
Alex Gunning deposited $25,000 with International Bank for four years and nine months. The bank has been paying interest at the rate of 8% per annum on a compound interest basis. Let us calculate the terminal balance.
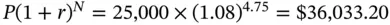
In the earlier case, when we assumed simple interest, we got a value of $34,500.
As can be seen from the examples, compounding yields substantially greater benefits than simple interest. And since the rate of interest is taken to the power of N , the larger the value of N , the greater will be the impact of compounding. In other words, the earlier one starts investing, the greater will be the returns.
Читать дальше