In real life, however, price levels are not constant, and inflation is a constant fact of life. Assume that the price of chocolates after a year is $12.50. If so, the $100 of interest that will be received as cash will be adequate to buy only eight boxes of chocolates. The principal itself will be adequate to buy only 80 boxes of chocolates, which means that the investor can acquire only 88 boxes in total. Thus, while the return on investment in terms of money is 10%, in terms of the ability to buy goods, it is –12%.
Assets such as Treasury securities give us returns in terms of money, without any assurance as to what our ability to acquire goods and services will be at the time of repayment. The rate of return yielded by such securities in dollar terms is termed as the nominal , or the money rate of return. In our illustration the investor got a 10% return on an investment of $1,000. In the situation where the price of a box of chocolates remained at $10, the ability to buy chocolates was enhanced by 10% and consequently the real rate was also 10%. However, when the price of chocolates rose to $12.50 per box, an initial investment of $1,000, which represented an ability to buy 100 boxes of chocolates at the outset, was translated into an ability to buy only 88 boxes at the end of the year. Thus, the real rate of return in this case was negative or was –12% to be precise.
The relationship between the nominal and real rates of return is called the Fisher Hypothesis , after the economist who first postulated it.
Let us consider a hypothetical economy which is characterized by the availability of a single good, namely chocolates. The current price of a box is $ P 0. Thus, one dollar is adequate to buy 1/ P 0boxes of chocolates at today's prices. Let the price of a box after a year be $ P 1.Assume that while P 1is known with certainty right from the outset, it need not be equal to P 0. In other words, although we are allowing for the possibility of inflation, we are assuming that there is no uncertainty regarding the rate of inflation. If the price of a box at the end of the year is P 1, one dollar will be adequate to buy 1/ P 1boxes after a year.
Let us assume that there are two types of bonds that are available to a potential investor. There is a financial bond that will pay $(1 + R ) next period per dollar that is invested now, and then there is a goods bond which will return (1 + r ) boxes of chocolates next period per box that is invested today. An investment of one dollar in the financial bond will give the investor dollars (1 + R ) next period, which will be adequate to buy (1 + R )/ P 1boxes. Similarly, an investment of one dollar in the goods bond or 1/ P 0boxes in terms of chocolates will yield (1 + r )/ P 0boxes after a year.
In order for the economy to be in equilibrium, both the bonds must yield identical returns. Thus, we require that
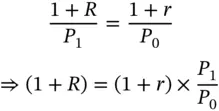
Inflation is defined as the rate of change in the price level. If we denote inflation by π, then
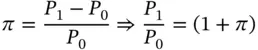
Therefore

This is the Fisher equation. R or the return on the financial bond is the nominal rate of return, while r or the rate of return on the goods bond is the real rate of return. Thus, the relationship is that one plus the nominal interest rate is equal to the product of one plus the real interest rate and one plus the rate of inflation. If the real rate of interest and the rate of inflation are fairly small, then the product 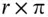 will be of a much smaller order of magnitude. For instance, if r = 0.03 and
will be of a much smaller order of magnitude. For instance, if r = 0.03 and 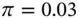 , then
, then 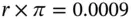 . If so, we can ignore the product term and rewrite the expression as
. If so, we can ignore the product term and rewrite the expression as
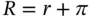
This is called the approximate Fisher relationship.
In Example 2.1, the nominal rate of return was 10% while the rate of inflation was 25%. Thus, the real rate was 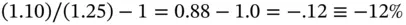 .
.
SIMPLE INTEREST & COMPOUND INTEREST
Before analyzing interest computation techniques, let us first define certain key terms.
Measurement Period: The unit in which time is measured for the purpose of stating the rate of interest is called the measurement period. The most common measurement period is one year, and we will use a year as the unit of measurement unless otherwise specified. That is, we will typically state that the interest rate is x%, say 10%, where the implication is that the rate of interest is 10% per annum.
Interest Conversion Period: The unit of time over which interest is paid once and is reinvested to earn additional interest is referred to as the interest conversion period. The interest conversion period will typically be less than or equal to the measurement period. For instance, the measurement period may be a year, whereas the interest conversion period may be three months. Thus, interest is compounded every quarter in this case.
Nominal Rate of Interest: The quoted rate of interest per measurement period is called the nominal rate of interest. For instance, in Example 2.1the nominal rate of interest is 10%.
Effective Rate of Interest: The effective rate may be defined as the interest that a dollar invested at the beginning of a measurement period would have earned by the end of the period. Quite obviously the effective rate will be equal to the quoted or nominal rate if the length of the interest conversion period is the same as that of the measurement period, which means that interest is compounded only once per measurement period. However, if the interest conversion period is shorter than the measurement period – or in other words, if interest is compounded more than once per measurement period – then the effective rate will exceed the nominal rate of interest. Take the case where the nominal rate is 10% per annum. If interest is compounded only once per annum, an initial investment of $1 will yield $1.10 at the end of the year, and we would say that the effective rate of interest is 10% per annum. However, if the nominal rate is 10% per annum, but interest is credited every quarter, then the terminal value of an investment of one dollar will definitely be more than $1.10. The relationship between the effective rate and the nominal rate will be derived subsequently. It must be remembered that the term nominal rate of interest is being used in a different context than in the earlier discussion where it was used in the context of the real rate of interest. The potential for confusion is understandable yet unavoidable.
Читать дальше

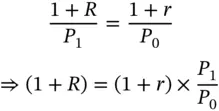
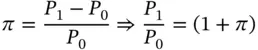

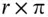 will be of a much smaller order of magnitude. For instance, if r = 0.03 and
will be of a much smaller order of magnitude. For instance, if r = 0.03 and 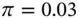 , then
, then 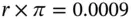 . If so, we can ignore the product term and rewrite the expression as
. If so, we can ignore the product term and rewrite the expression as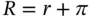
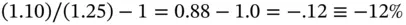 .
.










