Abdullah Eroglu - RF/Microwave Engineering and Applications in Energy Systems
Здесь есть возможность читать онлайн «Abdullah Eroglu - RF/Microwave Engineering and Applications in Energy Systems» — ознакомительный отрывок электронной книги совершенно бесплатно, а после прочтения отрывка купить полную версию. В некоторых случаях можно слушать аудио, скачать через торрент в формате fb2 и присутствует краткое содержание. Жанр: unrecognised, на английском языке. Описание произведения, (предисловие) а так же отзывы посетителей доступны на портале библиотеки ЛибКат.
- Название:RF/Microwave Engineering and Applications in Energy Systems
- Автор:
- Жанр:
- Год:неизвестен
- ISBN:нет данных
- Рейтинг книги:5 / 5. Голосов: 1
-
Избранное:Добавить в избранное
- Отзывы:
-
Ваша оценка:
RF/Microwave Engineering and Applications in Energy Systems: краткое содержание, описание и аннотация
Предлагаем к чтению аннотацию, описание, краткое содержание или предисловие (зависит от того, что написал сам автор книги «RF/Microwave Engineering and Applications in Energy Systems»). Если вы не нашли необходимую информацию о книге — напишите в комментариях, мы постараемся отыскать её.
An essential text with a unique focus on RF and microwave engineering theory and its applications RF/Microwave Engineering and Applications in Energy Systems,
RF/Microwave Engineering and Applications in Energy Systems

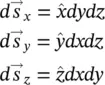
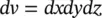
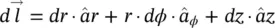
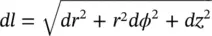
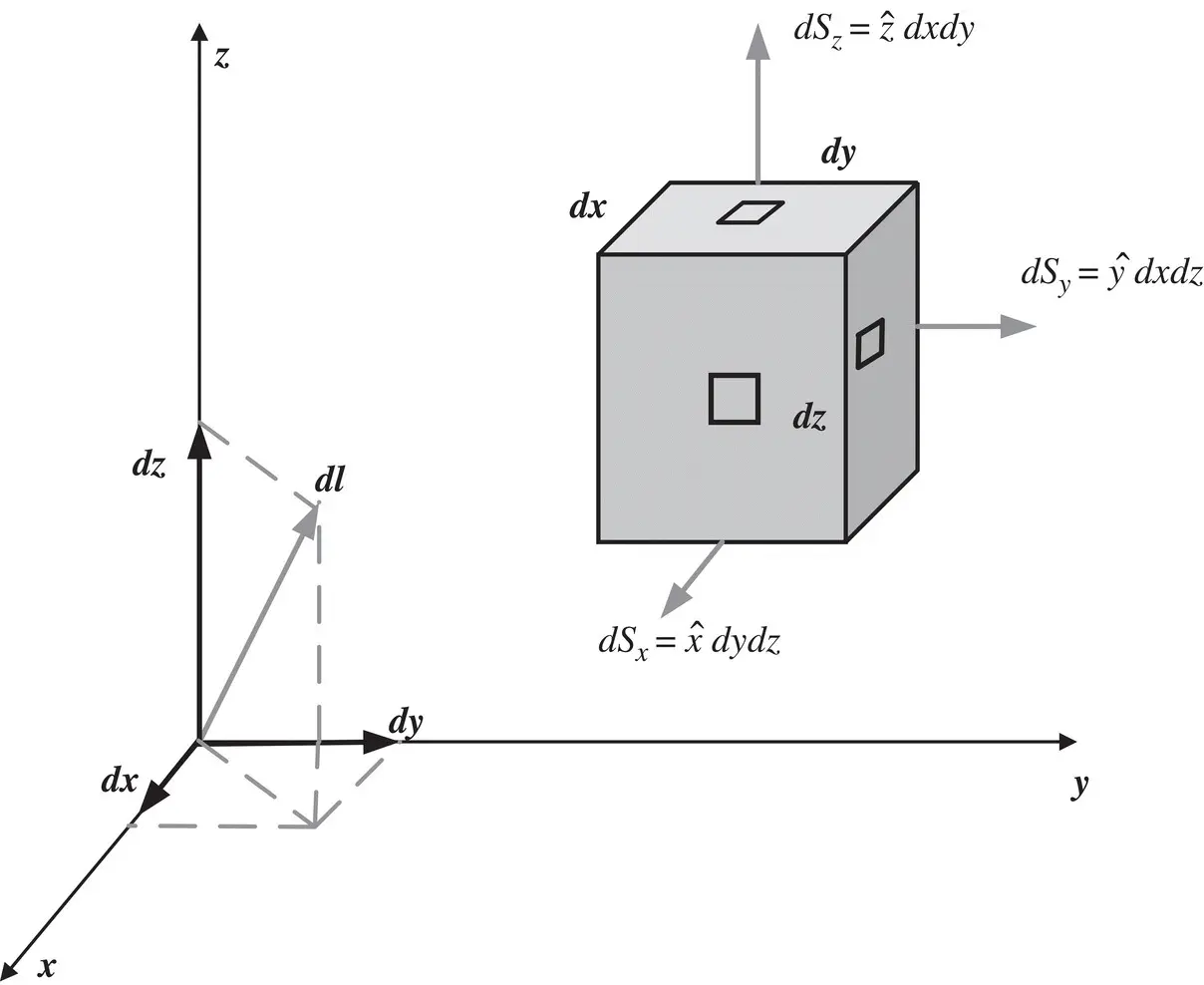
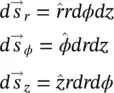
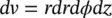
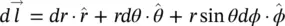
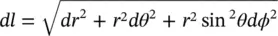
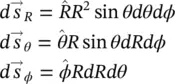
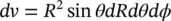
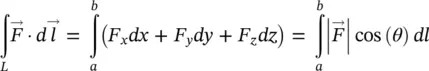
 .
.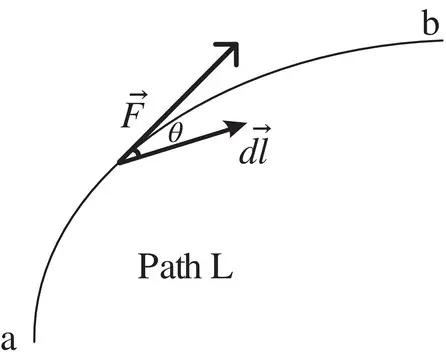
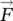 along the curve.
along the curve.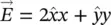 along the path given in Figure 1.13.
along the path given in Figure 1.13.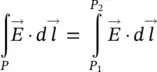
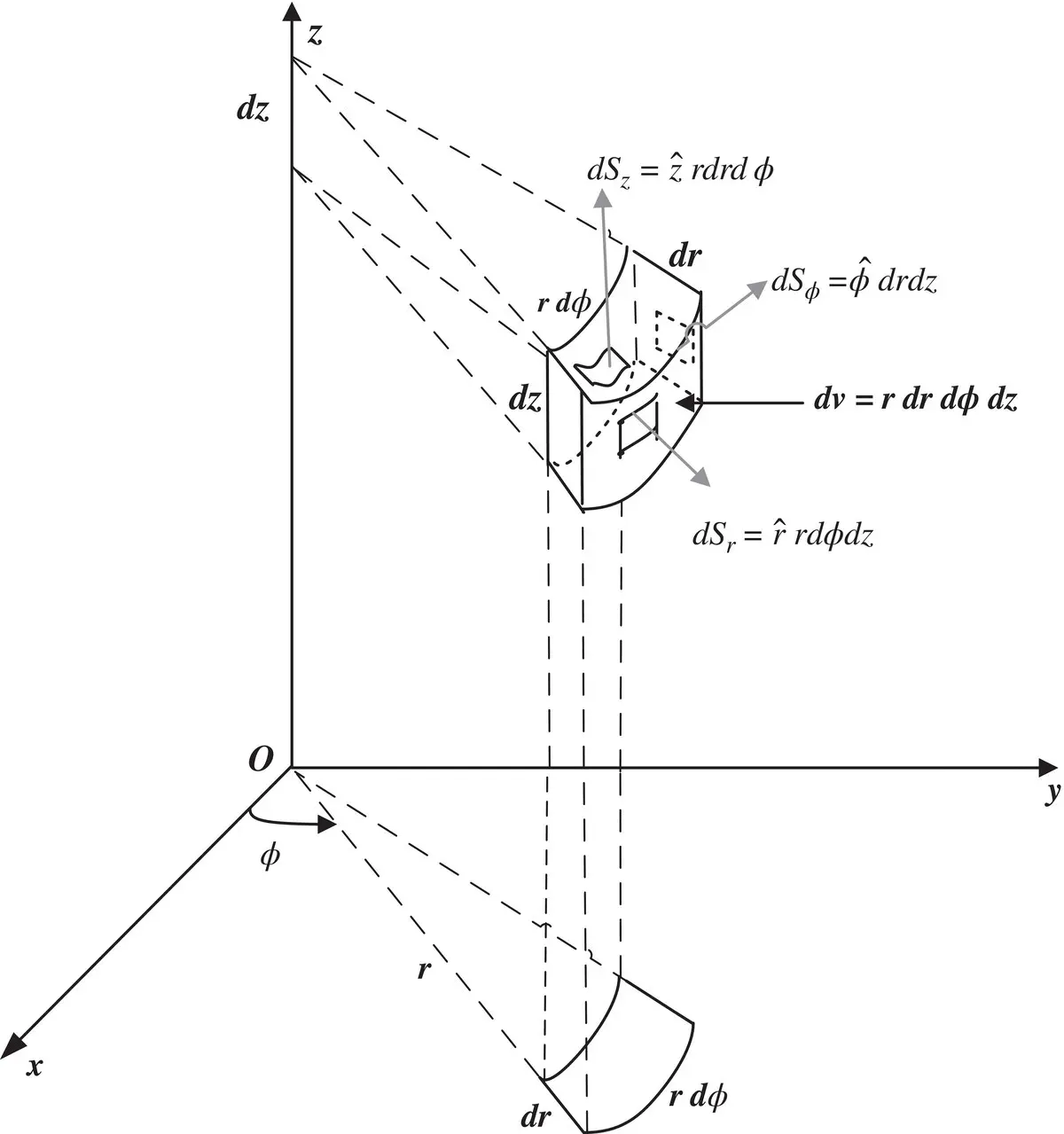
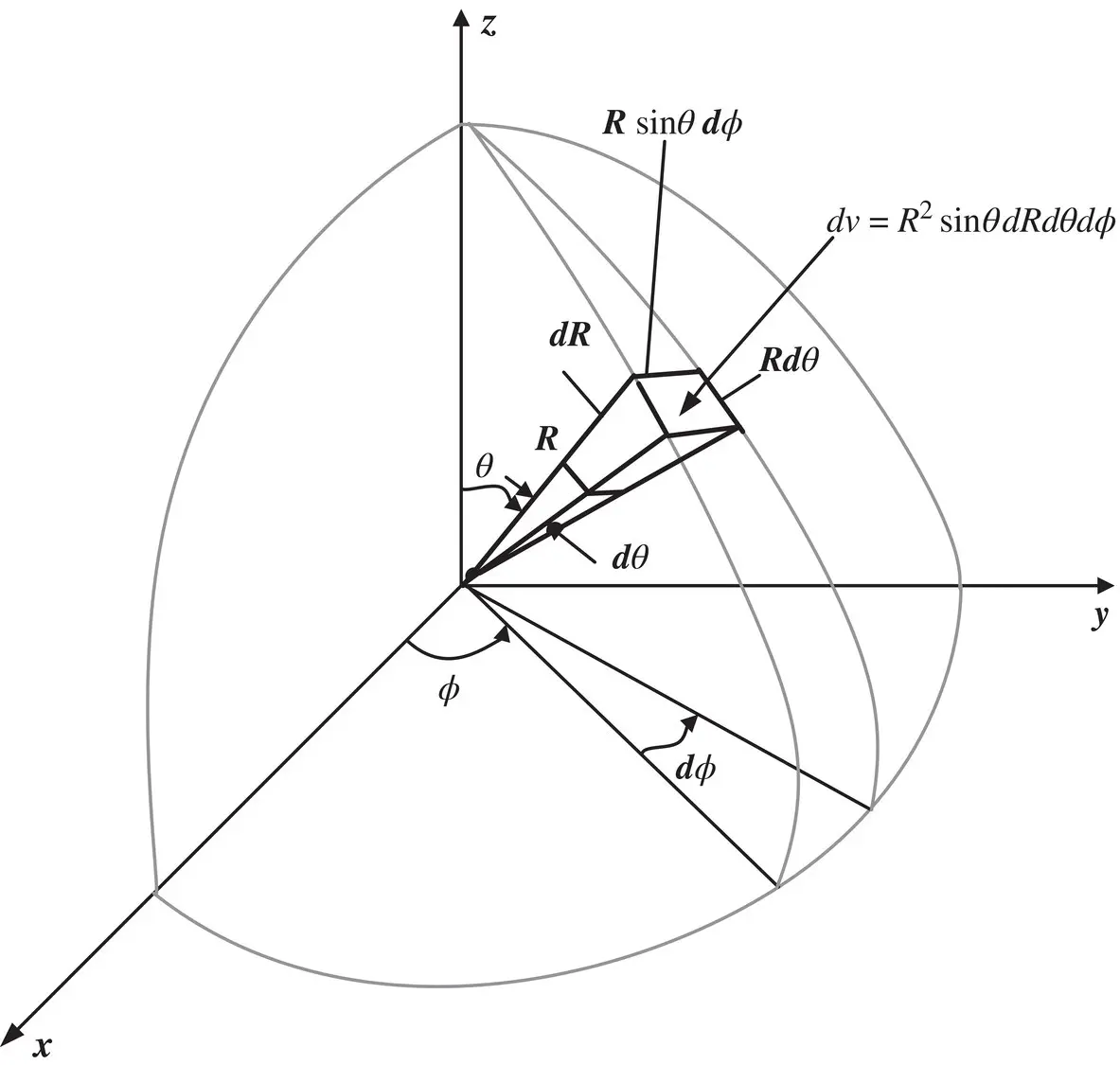
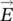 to cylindrical coordinates as
to cylindrical coordinates as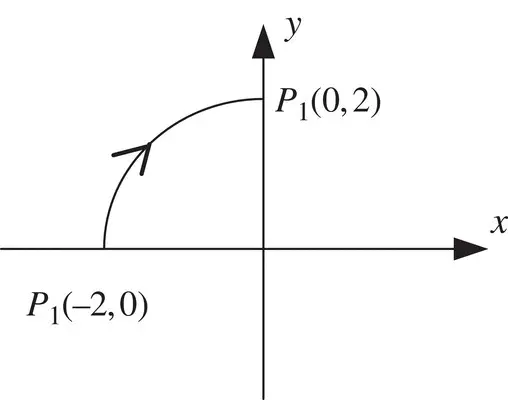
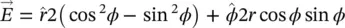
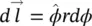
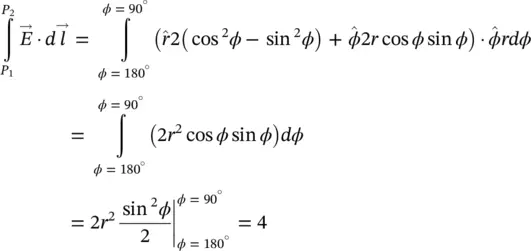
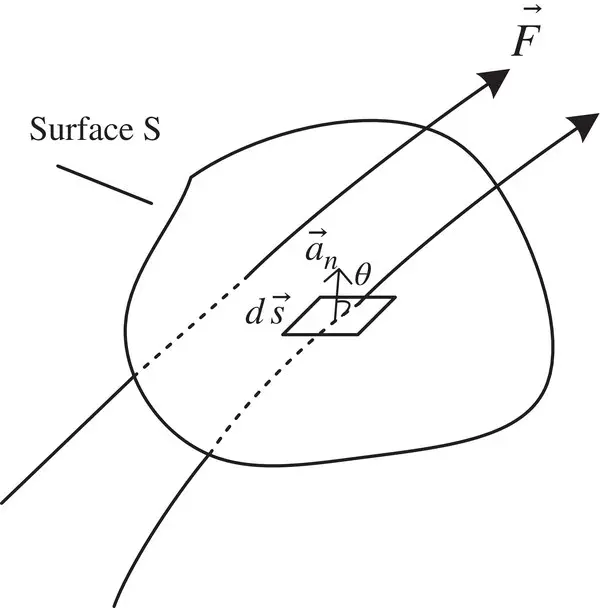
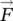 through surface S and expressed as
through surface S and expressed as










