Savo G. Glisic - Artificial Intelligence and Quantum Computing for Advanced Wireless Networks

83 83 Bedington, R., Arrazola, J.M., and Ling, A. (2017). Progress in satellite quantum key distribution. NPJ Quantum Inf. 3 (1): 30.

84 84 M. Pfennigbauer, W. Leeb, and M. Aspelmeyer, “Free‐space optical quantum key distribution using intersatellite links,” in Proc. CNESIntersatellite Link Workshop, 2003.

85 85 Huang, D. et al. (2020). Quantum key distribution over double‐layer quantum satellite networks. IEEE Access 8: 16087–16098. IEEE.

86 86 Pratt, S.R., Raines, R.A., Fossa, C.E., and Temple, M.A. (1999). An operational and performance overview of the IRIDIUM low earth orbit satellite system. IEEE Commun. Surv. Tuts. 2 (2): 2–10, 2nd Quart.

87 87 Bourgoin, J.‐P., Meyer‐Scott, E., Higgins, B.L. et al. (2013). A comprehensive design and performance analysis of low earth orbit satellite quantum communication. New J. Phys. 15 (2): 023006.

88 88 Günthner, K., Khan, I., Elser, D. et al. (2017). Quantum‐limited measurements of optical signals from a geostationary satellite. Optica 4 (6): 611–616.

89 89 Calderaro, L., Agnesi, C., Dequal, D. et al. (2018). Towards quantum communication from global navigation satellite system. Quantum Sci. Technol. 4 (1): 015012.

90 90 F. Yu. ScienceNet.cn, China. Accessed: Aug. 10, 2017. [Online]. Available: http://news.sciencenet.cn/htmlnews/2017/8/384831.shtm?id=384831. http://news.sciencenet.cn/htmlnews/2017/8/384831. 中国科学家࣋划建“量子星座”—新闻—科学网 (sciencenet.cn)

91 91 Kimble, H.J. (2008). The quantum internet. Nature 453 (7198): 1023–1030.

92 92 Nguyen, H.V. et al. (2017). Towards the quantum internet: generalized quantum network coding for large‐scale quantum communication networks. IEEE Access 5: 17288–17308.

93 93 Sun, Q.‐C. et al. (2016). Quantum teleportation with independent sources and prior entanglement distribution over a network. Nat. Photon. 10 (10): 671–675.

94 94 Yin, J. et al. (2017). Satellite‐based entanglement distribution over 1200 kilometers. Science 356 (6343): 1140–1144.

95 95 Briegel, H.‐J., Dür, W., Cirac, J.I., and Zoller, P. (1998). Quantum repeaters: the role of imperfect local operations in quantum communication. Phys. Rev. Lett. 81: 5932–5935.

96 96 Dür, W., Briegel, H.‐J., Cirac, J.I., and Zoller, P. (1999). Quantum repeaters based on entanglement purification. Phys. Rev. A Gen. Phys. 59: 169–181.

97 97 Żukowski, M., Zeilinger, A., Horne, M.A., and Ekert, A.K. (Dec. 1993). “Event‐readydetectors” bell experiment via entanglement swapping. Phys. Rev. Lett. 71: 4287–4290.

98 98 Deutsch, D. et al. (1996). Quantum privacy amplification and the security of quantum cryptography over noisy channels. Phys. Rev. Lett. 77: 2818–2821.

99 99 Wootters, W.K. and Zurek, W.H. (1982). A single quantum cannot be cloned. Nature 299 (5886): 802–803.

100 100 Dieks, D. (1982). Communication by EPR devices. Phys. Rev. A Gen. Phys. 92 (6): 271–272.

101 101 Bennett, C.H., Brassard, G., Crépeau, C. et al. (Mar. 1993). Teleporting an unknown quantum state via dual classical and Einstein‐Podolsky‐Rosen channels. Phys. Rev. Lett. 70: 1895–1899.

102 102 Van Meter, R. (2014). Quantum Networking. Wiley.

103 103 Lloyd, S., Shapiro, J.H., Wong, F.N. et al. (2004). Infrastructure for the quantum internet. ACM SIGCOMM Computer Commun. Rev. 34 (5): 9–20.

104 104 Castelvecchi, D. (2018). The quantum internet has arrived (and it hasn't). Nature 554 (7692): 289.

105 105 Bennett, C.H. and Brassard, G. (2014). Quantum cryptography: public key distribution and coin tossing. Theor. Comput. Sci. 560 (P1): 7–11.

106 106 Ekert, A.K. (1991). Quantum cryptography based on bell theorem. Phys. Rev. Lett. 67 (6): 661.

107 107 Broadbent, A. and Schaffner, C. (2016). Quantum cryptography beyond quantum key distribution. Des. Codes Cryptogr. 78 (1): 351–382.

108 108 Wehner, S., Elkouss, D., and Hanson, R. (2018). Quantum internet: a vision for the road ahead. Science 362 (6412): eaam9288.

109 109 Van Meter, R., Ladd, T.D., Munro, W., and Nemoto, K. (2009). System design for a long‐line quantum repeater. IEEE/ACM Trans. Netw. (TON) 17 (3): 1002–1013.

110 110 Simon, C., De Riedmatten, H., Afzelius, M. et al. (2007). Quantum repeaters with photon pair sources and multimode memories. Phys. Rev. Lett. 98 (19): 190503.

111 111 Sangouard, N., Dubessy, R., and Simon, C. (2009). Quantum repeaters based on single trapped ions. Phys. Rev. A 79 (4): 042340.

112 112 M. A. Nielsen and I. Chuang, “Quantum computation and quantum information,” 2002.

113 113 Bennett, C.H., Brassard, G., Crepeau, C. et al. (1993). Teleporting an unknown quantum state via dual classical and Einstein‐Podolsky‐Rosen channels. Phys. Rev. Lett. 70 (13): 1895.

114 114 Caleffi, M. (2017). Optimal routing for quantum networks. IEEE Access 5: 22 299–22 312.

115 115 Gyongyosi, L. and Imre, S. (2018). Decentralized base‐graph routing for the quantum internet. Phys. Rev. A 98 (2): 022310.

116 116 Van Meter, R., Satoh, T., Ladd, T.D. et al. (2013). Path selection for quantum repeater networks. Netw. Sci. 3 (1–4): 82–95.

117 117 Perseguers, S., Lapeyre, G. Jr., Cavalcanti, D. et al. (2013). Distribution of entanglement in large‐scale quantum networks. Rep. Prog. Phys. 76 (9): 096001.

In the first subsection of this chapter, we briefly present a number of machine learning (ML) algorithms in a rather descriptive way. Only in the second subsection will we go into the details of a limited subset of these algorithms. Due to the massive interest in neural networks, this topic is presented in detail separately in Chapters 3– 5.

Regression analysis deals with the problem of fitting straight lines to patterns of data. In a linear regression model, the variable of interest (the so‐called “dependent” variable) is predicted from k other variables (the so‐called “independent” variables) using a linear equation. If Y denotes the dependent variable and X 1, …, X k, are the independent variables, then the assumption is that the value of Y at time t is determined by the linear equation

(2.1)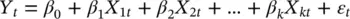

The corresponding equation for predicting Y tfrom the corresponding values of the X ’s is therefore

(2.2)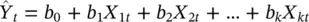

where the b ’s are estimates of the betas obtained by least squares, that is, minimizing the squared prediction error within the sample. This is about the simplest possible model for predicting one variable from a group of others, and it rests on the assumption that the expected value of Y is a linear function of the X variables. More precisely, the following is assumed:

1 The expected value of Y is a linear function of the X variables. This means: (i) If Xi changes by an amount ∆Xi, holding other variables fixed, then the expected value of Y changes by a proportional amount βi∆Xi, for some constant βi (which in general could be a positive or negative number). (ii) The value of βi is always the same, regardless of values of the other X’s. (iii) The total effect of the X’s on the expected value of Y is the sum of their separate effects.

2 The unexplained variations of Y are independent random variables (in particular, not “autocorrelated” if the variables are time series).