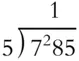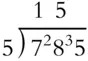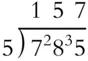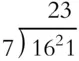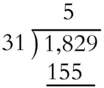1 Add 453 and 975.
2 Find the sum of 1,864 and 798.
3 Multiply 561 by 92.
4 What is the product of 891 and 30?
5 Multiply 135 × 112.
If the first two gave you trouble, review Frame 1. If you got any of the last three wrong, review Frame 2. If you've got this, move on!
Subtraction is the inverse, or opposite, of addition. Addition puts together. Subtraction takes apart. If you buy a carton of 12 eggs and you use 4 of them to make breakfast, how many eggs are left? 12 – 4 = 8 if you count the remaining eggs. That subtraction problem is another way of thinking about the addition problem 4 + 8 = 12. Each subtraction problem has a related addition problem. 17 – 9 = ? is related to 9 + what = 17? Sometimes it's easier to think about the addition version. If you have 9 and you want 17, you need 1 to make 10 and then 7 more to get up to 17. That's a total of 8.
For larger problems, you'll work column by column, starting from the ones, just like addition, but sometimes you'll need to “borrow,” which means you'll regroup but in the other direction.
In the following example, the ones column is easy: 8 – 3 = 5. But trying to take 9 away from 3 in the tens column is a problem. If you only have 3, how can you take away 9? (There's more than one answer to that question. We'll look at one now and another one in Chapter 6, “Positive and Negative Numbers.”)
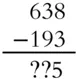
We only have 3 tens in our tens column, and we need more, so we're going to borrow 1 hundred from the hundreds column and exchange it for 10 tens. There are 6 hundreds, so if we borrow 1, there will be 5 left. We'll exchange the 1 hundred for 10 tens and add them to our 3 tens so we have 13 tens. We can subtract 9 tens from 13 tens and get 4 tens, then subtract 1 hundred from the remaining 5 hundreds to get 4 hundreds.
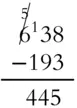
Subtract 124 from 896.
Solution:
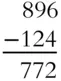
This subtraction doesn't require any regrouping. Just subtract the digits in each column: 6 – 4 = 2, 9 – 2 = 7, and 8 – 1 = 7.
Find the difference between 293 and 581.
Solution:
To begin, you need to “borrow” and regroup, because you can't subtract 3 from 1. Remember that the 8 tens become 7 tens and the ten we borrowed is added to the 1. Subtract 3 from 11 to get 8.
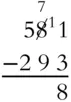
But this requires another regrouping. Borrow 1 from the 5 hundreds, leaving 4 hundreds, and change the borrowed hundred to 10 tens. Add that to the 7 (not 8) tens and subtract 9 from 17.
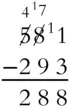
Finish by subtracting 2 hundred from the remaining 4 hundred.
Division is the opposite, or inverse, of multiplication. You can think of a division question like 21 ÷ 3 = ? as the related multiplication question 3 × what = 21? Sometimes memory is enough to answer that. You can also phrase the question as, “If you put 21 objects into groups of 3, how many groups can you make?” Another approach is to ask, “If 3 people share $21, how much does each person get?”
Division with larger numbers can get complicated. There are several methods, one of which is covered below. Others will come up in Chapter 4, “Focus on Division.” It's fair to say that division with larger numbers is one task for which calculators are helpful. If you're going to use a calculator, you'll want to be able to estimate the answer, so that you can see if the answer on the calculator is reasonable. Errors, even as simple as a typing error, can give you a wildly wrong answer.
When you use a calculator for division, it helps to have an idea of what a reasonable answer will look like. If you divide 3,482,603 by 274 and get an answer of 12, bells should go off to say that can't possibly be right. Why doesn't that sound right? Well, think about dividing with easier numbers. 3,482,603 is larger than 3,000,000 and 274 is around 300. 3,000,000 ÷ 300 = 10,000 so the answer to the actual problem should be in that neighborhood, which means 12 must be wrong. In fact, 3,482,603 ÷ 274 = 12,710 with a little left over.
In a division problem, you have a dividend, a divisor, a quotient, and a remainder. You don't need those labels all that often but we'll need them to talk about how to divide. If you want to divide 785 by 5, the 785 is the dividend and 5 is the divisor. If the dividend is large but the divisor is small, you can use what's called short division. It's a method that uses regrouping and compresses the work.
Set up with the dividend inside and the divisor outside, like this: 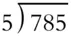 . Look at the first digit in the dividend, 7. Can you divide 7 by 5? There is one 5 and 2 left over. Show that like this:
. Look at the first digit in the dividend, 7. Can you divide 7 by 5? There is one 5 and 2 left over. Show that like this:
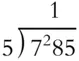
Those 2 hundreds that were left get regrouped as 20 tens so now that middle number is not just 8 but 28. Divide 28 by 5, and you get 5 with 3 left over.
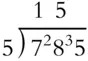
Divide 35 by 5 to get 7.
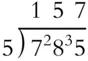
What is the result of dividing 161 by 7?
Solution:
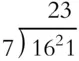
Divide 7 into 16. It goes twice, so place the 2 up top, but 7 × 2 = 14, so there will be 2 left over. Write the 2 beside the 1 and divide 7 into 21. That gives you 3.
Divide 1,829 by 31. Estimate first by thinking about 1,800 ÷ 30.
Solution:
Estimate your answer by thinking about how many times 30 could be subtracted from 1,800 or by thinking that 18 ÷ 3 = 6 and so 1,800 ÷ 30 would need a 6 and another zero. 1,800 ÷ 30 = 60, so expect a quotient close to 60. This one may be hard to keep all in your head, so write down as you go.
You're probably tempted to start with a 6, but if you check 6 × 31 = 186, and you're trying to divide into 182, so 6 is too big. Drop down to 5, and place 5 × 31 = 155 under the 182.
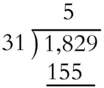
Subtract 182 – 155 = 27 and bring down the 9. Three goes into 27 nine times so there's a good chance 31 goes into 279 nine times. Multiply to check it.
Читать дальше

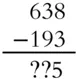
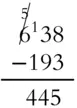
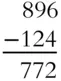
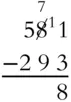
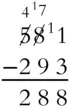
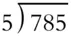 . Look at the first digit in the dividend, 7. Can you divide 7 by 5? There is one 5 and 2 left over. Show that like this:
. Look at the first digit in the dividend, 7. Can you divide 7 by 5? There is one 5 and 2 left over. Show that like this: