Steve Slavin - All the Math You'll Ever Need

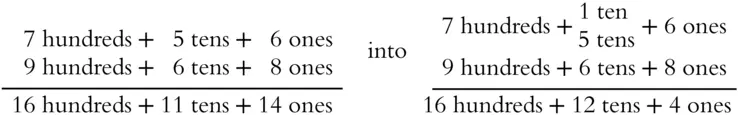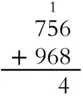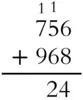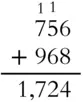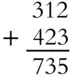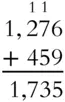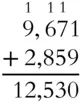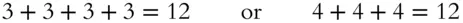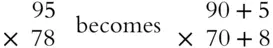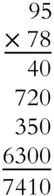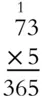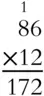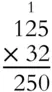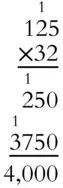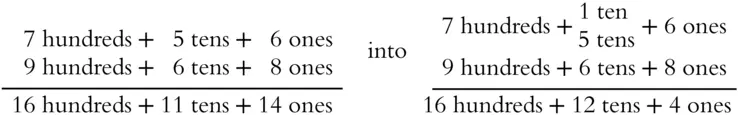
You'll do the same sort of regrouping with the 12 tens. Ten of those tens make 1 hundred, leaving 2 tens in the tens place. You can do this without using the expanded form. Add 6 + 8 to get 14. Put down the 4 and carry the one ten.

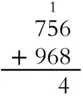
Add 1 + 5 + 6 to get 12. Put down the 2 (tens) and carry the 1 (hundred).

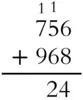
Add 1 + 7 + 9 to get 17. The 7 goes in the hundreds place and the 1 (thousand) slides into the thousands place.

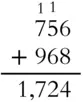
Add 312 and 423.

Solution:

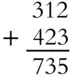
All that's necessary is adding the digits in each column: 2 + 3 = 5, 1 + 2 = 3, and 3 + 4 = 7.

What is the result when 459 is added to 1,276?

Solution:

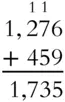
This one requires a little bit of regrouping. Add 6 + 9 to get 15, put down the 5 and carry 1 to the next column. Then 7 + 5 is 12, plus the 1 you carried is 13. Put down the 3 and carry the 1. You can think of the rest as 2 + 4 + 1 = 7 and the 1 thousand comes down unchanged, or you can think of it as 12 + 4 is 16, plus 1 you carried is 17.

What is the combined total of 9,671 and 2,859?

Solution:

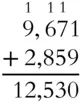
Here again you're regrouping. In the ones column, 1 + 9 is 10, so put down the 0 and carry the 1. Then 7 + 5 is 12 plus 1 you carried makes 13. Put down the 3 and carry the 1. Add 6 + 8 + 1 to get 15. Put down the 5 and carry the 1. Finally, 9 + 2 + 1 is 12.

Multiplication is repeated addition. For instance, you probably know 4 × 3 is 12 because you searched your memory for that multiplication fact. There's nothing wrong with that.

Another way to calculate 4 × 3 is to think of it as adding four threes, or adding three fours.

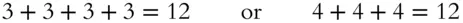
What about 5 × 7? Maybe you know it's 35, but you could always do this:

You do multiplication instead of addition because it's shorter—sometimes much shorter. Suppose you needed to multiply 78 × 95. If you set this up as an addition problem, you'd have to write 78 copies of 95 before you could even start adding.

Let's set this up as a regular multiplication problem and take a look at the expanded form.

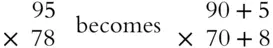
The key to this multiplication is you have to multiply 8 × 5 and 8 × 90 and then multiply 70 × 5 and 70 × 90, and add up all the results. Don't get discouraged, because there is a condensed form.

The first set of numbers we'd multiply would be 8 × 5. You probably know, or can figure out, that's 40. (We'll focus on all the multiplication facts you should memorize in Chapter 3, “Focus on Multiplication.”) Then we'd multiply 8 × 90, which just means multiplying 8 × 9 and putting a zero at the end. Whenever you multiply a number that ends in zero, you can deal with the non-zero parts and add the zero at the end. (See Chapter 5, “Mental Math” for more on that shortcut.) 8 × 9 =72 so 8 × 90 = 720. Next would come 70 × 5. 7 × 5 = 35 so 70 × 5 =350. The last multiplication would be 70 × 90. Multiply 7 × 9 = 63, and then add a zero for the 70 and another zero for the 90. 70 × 90 = 6,300. Add up 6,300 + 350 + 720 + 40 to get 7,410.

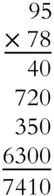
Here's how to write it more compactly. Multiply 8 × 5 = 40, put down the 0 and carry the 4. 8 × 9 = 72 and the 4 we carried makes 76. Write the 76 in front of that 0 you put down and you see 760. This 760 is the 40 and the 720 combined. Now, you need to multiply 95 by 70, which means multiply by 7 and add a zero. So put the zero down first, under the 0 of the 760. Then 7 × 5 = 35. Put down the 5 to the left of the 0 and carry the 3. 7 × 9 = 63 plus the 3 you carried is 66. Write the 66 in front of the 50 and you've got 6,650, which is the 350 and 6300 combined. Add the two lines, and you're done.

As you can see, a long multiplication problem can be broken down into a series of simple multiplication problems. It's important to have basic multiplication facts in memory, so you don't have to spend time doing the repeated addition every time. You'll learn more about that in the next chapter.

Multiply 73 by 5.

Solution:

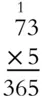
Begin with 5 × 3 = 15. Put down the 5 and carry 1. Then 5 × 7 is 35 plus the 1 you carried is 36.

Find the product of 86 and 12.

Solution:

First multiply 86 by 2.

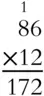
Multiplying 2 × 6 gives you 12, so put down the 2 and carry 1. Then 2 × 8 is 16 plus 1 you carried is 17.

Place a zero at the end of the second line, or if you prefer, just move one space right, and multiply 1 × 86, which obviously is 86. Add the columns to complete the job.

What is the result when 125 is multiplied by 32?

Solution:

Multiplying 125 by 2 requires a little bit of carrying.

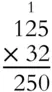
Place a zero on the second line, or move one space right, then multiply 3 × 125. Add down each column, regrouping where necessary.

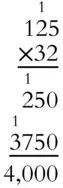
Ready to test yourself? Try Self-Test 2.1.