12 9.First, find the difference of the numbers in the absolute value symbols. The sign of the difference is negative because 13 is farther from 0 than 4 on the number line. Evaluating the absolute value gives you a positive result: 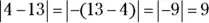 .
.
13 −16.Drop the negative signs and find the sum of the two numbers. The answer is negative, because the signs are the same:  .
.
14 8.Change the problem to addition and the negative 14 to a positive number. Then, because the signs are different, find the difference. The answer is positive because 14 is farther from 0 than 6 on the number line: 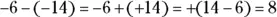 .
.
15 −40.Drop the negative sign and multiply. The answer is negative, because the signs are different: 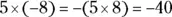 .
.
16 1.Find the difference between the two numbers, because the signs are different. The answer is positive, because 8 is farther from 0 than 7 on the number line: 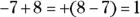 .
.
17 5.First, find the difference. Then apply the absolute value operation: 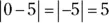 .
.
18 2.Change the subtraction to addition and the negative 4 to +4. Then find the difference, because the signs are different. The answer is positive, because 4 is farther from 0 than 2 on the number line: 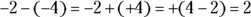 .
.
19 2.Find the difference, because the signs are different. The answer is positive, because 5 is farther from 0 than 3 on the number line: 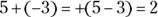 .
.
20 −119.Change the subtraction to addition and make the 62 a negative number. Ignore the signs when you add the two numbers with the same sign. The sum is negative, because the signs are the same: 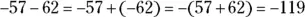 .
.
21 157.Change the problem to addition and the negative 84 to a positive number. Then, because the signs are different, find the sum: 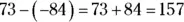 .
.
22 38.Find the difference, because the signs are different. The answer is positive, because 90 is farther from 0 on the number line: 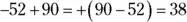 .
.
23 263.First, find the difference, and then apply the absolute value operation. The difference will be negative, because 330 is negative and it’s farther from 0 on the number line. The absolute value operation makes the result positive: 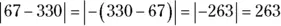 .
.
24 143.Drop the negative signs and multiply. The answer is positive, because the signs are the same: 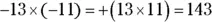 .
.
25 −20.Drop the negative sign and divide. The answer is negative, because the signs are different: 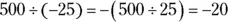 .
.
26 −48.Find the difference, because the signs are different. The answer is negative, because 72 is farther from 0 on the number line: 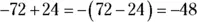 .
.
Chapter 5
Putting the Big Four Operations to Work
IN THIS CHAPTER
 Working with the Big Four operations (addition, subtraction, multiplication, and division)
Working with the Big Four operations (addition, subtraction, multiplication, and division)
 Identifying which operations are inverses of each other
Identifying which operations are inverses of each other
 Knowing the operations that are commutative, associative, and distributive
Knowing the operations that are commutative, associative, and distributive
 Performing the Big Four operations on negative numbers
Performing the Big Four operations on negative numbers
 Using four symbols for inequality
Using four symbols for inequality
 Understanding exponents, roots, and absolute values
Understanding exponents, roots, and absolute values
When you understand the Big Four operations — adding, subtracting, multiplying, and dividing — you can begin to look at math on a whole new level. In this chapter, you extend your understanding of the Big Four operations and move beyond them. I begin by focusing on four important properties of the Big Four operations: inverse operations, commutative operations, associative operations, and distribution. Then I show you how to perform the Big Four on negative numbers.
I continue by introducing you to some important symbols for inequality. Finally, you’re ready to move beyond the Big Four by discovering three more advanced operations: exponents (also called powers ), square roots (also called radicals ), and absolute values.
Switching Things Up with Inverse Operations and the Commutative Property
Читать дальше

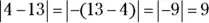 .
. .
.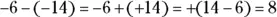 .
.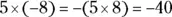 .
.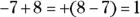 .
.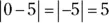 .
.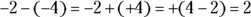 .
.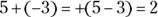 .
.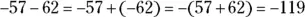 .
.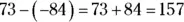 .
.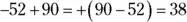 .
.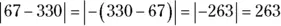 .
.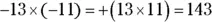 .
.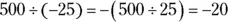 .
.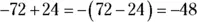 .
. Working with the Big Four operations (addition, subtraction, multiplication, and division)
Working with the Big Four operations (addition, subtraction, multiplication, and division)










