Using the standard basis, the basis states for a two-qubit system are defined by combinations of the |0⟩ and |1⟩ states:
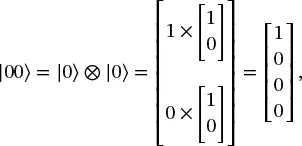 (1.33)
(1.33)
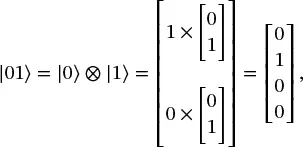 (1.34)
(1.34)
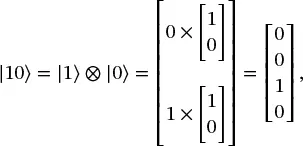 (1.35)
(1.35)
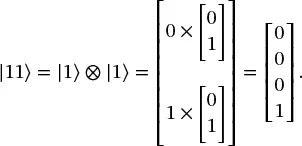 (1.36)
(1.36)
Any two-qubit state can be written as a linear combination of the basis states:
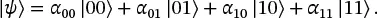 (1.37)
(1.37)
Two-qubit state vectors are also normalized:
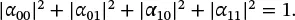 (1.38)
(1.38)
As we will see later, while every two-qubit state can be written in the form of Eq. ( 1.37), not every two-qubit state can be written as the tensor product of single-qubit states.
This can be generalized into a system with n qubits, requiring state vectors with 2 ncomponents with 2 ncomplex coefficients.
1.5.2 Matrix Representation of Two-Qubit Gates
Just as single qubit gates can be represented by 2×2 matrices, an n -qubit gate can be represented by a 2n×2n matrix. Consequently two-qubit gates require the construction of 4×4 unitary matrices. Given two single-qubit operators A and B , the tensor product is defined as:
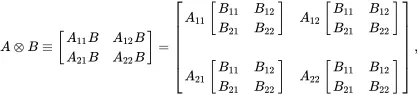 (1.39)
(1.39)
which creates a 4×4 matrix.
Suppose we wanted to construct a two-qubit circuit starting in the state |10⟩ with an X gate applied to the left qubit, and a Y gate applied to the other. Mathematically this would be written
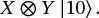 (1.40)
(1.40)
Referring to ( 1.24) we see that the X gate will simply flip the left qubit, and referring to ( 1.25) we see that the Y gate will flip the right qubit and add the coefficient i . We conclude that
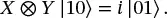 (1.41)
(1.41)
To see how this would be implemented using the matrix representation, we first construct the X⊗Y matrix:
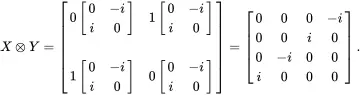 (1.42)
(1.42)
Completing the calculation gives the expected result:
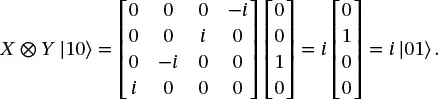 (1.43)
(1.43)
A particularly interesting two-qubit circuit is formed by applying a Hadamard gate to each qubit in the ground state: H ⊗ H |00⟩. Let us first compute H ⊗ H :
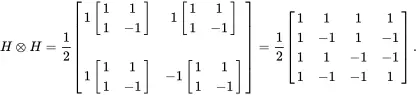 (1.44)
(1.44)
Completing the calculation gives:
 (1.45)
(1.45)
Note that the resulting state vector can be decomposed into a sum of all of the two-qubit basis states:
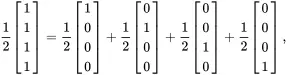 (1.46)
(1.46)
or alternatively
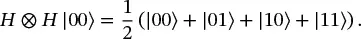 (1.47)
(1.47)
We see that application of Hadamard gates to each qubit creates an equally weighted superposition of all possible basis states. This is often a very useful starting point for a quantum calculation.
Although the matrix representation can be helpful in understanding the operations, calculations can often be done more compactly once the effect of the gates are understood. For example, we could write H ⊗ H |00⟩ = H ⊗ H |0⟩ |0⟩, apply the Hadamard gates to each qubit, and simplify:
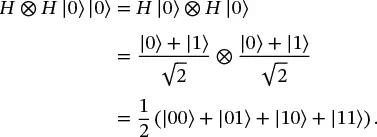 (1.48)
(1.48)
We conclude this section with a comment on notation. A more compact notation is often used for situations where the same operator is applied across multiple qubits; i.e., H⊗H is alternatively written H⊗2, H⊗H⊗H=H⊗3, etc.
The gates that we have considered so far involve operations that are independently applied to separate qubits—there is no qubit–qubit interaction. If we are to entangle two qubits, then we need classes of gates where the operation on one qubit depends on the state of another. One of the most important such gates is the controlled-NOT, or CNOT gate. For this gate, one of the input qubits is the “control,” and the other is the “target.” If the control qubit is zero, then nothing is done to the target qubit, but if the control qubit is one, then the target qubit is flipped. For example, if the right qubit in our notation is the control and the left qubit is the target, then the CNOT gate transforms the basis states as follows:
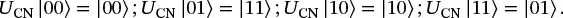 (1.49)
(1.49)
The effect of a CNOT can be compactly represented by UCN|t⟩|c⟩=|c⊕t⟩|c⟩, where ⊕ represents exclusive-OR or modulo-2 addition (e.g., 0+1=1, but 1+1=0). The matrix representation of the CNOT gate is
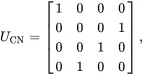 (1.50)
(1.50)
and the circuit symbol is shown in Figure 1.4.
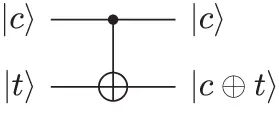
Figure 1.4 Symbol for a CNOT gate, and its effect on basis states.
It is worth noting at this point that we are putting the least-significant qubit at the top of a circuit diagram, and on the right on the state labels used with kets. This labels states with the natural binary order. However, there are different conventions in use, and this can be a point of confusion. Some authors put the top-most qubit in a circuit diagram on the left when they label kets. In this alternate notation, UCN′|c⟩|t⟩=|c⟩|c⊕t⟩ so that
Читать дальше

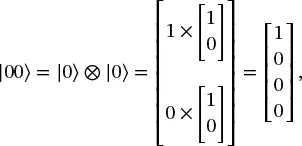 (1.33)
(1.33)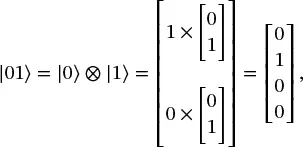 (1.34)
(1.34)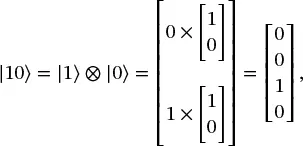 (1.35)
(1.35)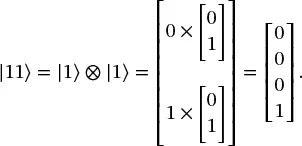 (1.36)
(1.36)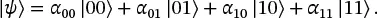 (1.37)
(1.37)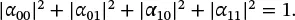 (1.38)
(1.38) (1.39)
(1.39)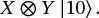 (1.40)
(1.40)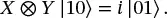 (1.41)
(1.41)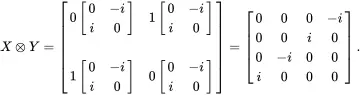 (1.42)
(1.42)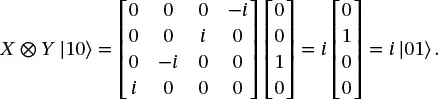 (1.43)
(1.43)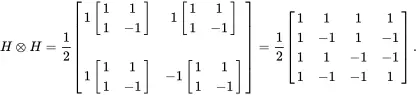 (1.44)
(1.44) (1.45)
(1.45)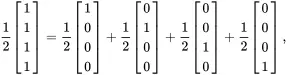 (1.46)
(1.46)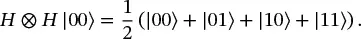 (1.47)
(1.47)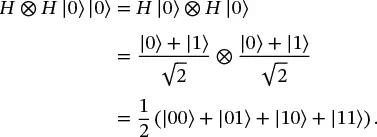 (1.48)
(1.48)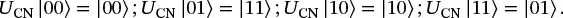 (1.49)
(1.49)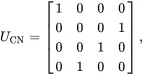 (1.50)
(1.50)




![Алексей Лавров - Quantum Ego [СИ]](/books/414972/aleksej-lavrov-quantum-ego-si-thumb.webp)



