Isotopic Constraints on Earth System Processes

Frank M. Richter

Department of the Geophysical Sciences, The University of Chicago, Chicago, Illinois, USA

Laboratory experiments were used to document kinetic isotope fractionation by mass transport in high‐temperature silicate materials. Large kinetic isotope fractionations were found in experiments in which basalt and rhyolite were juxtaposed and annealed in a piston cylinder assembly, and in experiments where the piston cylinder assembly was displaced from the furnace hot spot so that mass transport was also driven by differences in temperature (i.e., Soret diffusion). Another set of laboratory experiments showed, somewhat surprisingly, that diffusion in silicate minerals can be more effective at fractionating isotopes than diffusion in silicate melts. Isotope fractionations by diffusion in minerals are especially important in that they provide a new way of determining the degree to which diffusion was responsible for all, some, or none of the zoning of minerals from natural settings. Evaporation of silicate materials was an important process in the protoplanetary nebula. This motivated vacuum evaporation experiments that quantified the isotope fractionation associated with the amount of a parent element volatilized, allowing one to interpret the isotopic fractionation of early solar system materials in terms of mass loss by evaporation. A closing section gives some thoughts regarding future directions for research on high‐temperature kinetic isotope.

It has long been known from the kinetic theory of gases that the relative mobility of isotopes in a gas depends on their mass. In the limit of a rarefied gas with isotopes of mass m iand m jthe ratio of their diffusion coefficients is given by D i/ D j= ( m j/ m i) 0.5. In the case of a trace gas diffusing in a gas of molecular mass M the ratio of the isotope diffusion coefficients depends on the inverse square root of their reduced mass so that D i/ D j= ( μ j/ μ i) 0.5where 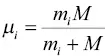and similarly for μ j. During the 1960s, physicists did a great deal of work documenting isotope fractionation by diffusion in metals, metal alloys, and metalloids (see Fig. 8 and references in Richter et al., 2009a) as a way of gaining insight into the mechanisms by which diffusion takes place in these materials. Experimental studies documenting kinetic isotope fractionation in silicate materials of interest to geochemistry and cosmochemistry did not start until much later.

The following sections discuss high‐temperature laboratory diffusion experiments that quantified kinetic isotopic fractionations associated with diffusion in silicate liquids and minerals. The results of these experiments are used to identify the processes responsible for chemical gradients in silicate materials from natural settings. Experiments quantifying kinetic isotope fractionation by evaporation from silicate liquids of interest to cosmochemistry are discussed in a final section. The experimental and analytical methods are only briefly described, and the interested reader will find them discussed in detail in the various papers referenced in connection with kinetic isotope fractionation in laboratory and natural samples.

Fick’s first law of diffusion

(1.1)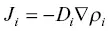

is often used to characterize the particle or molar flux J i(i.e., particles or moles of i per cm 2per second) in terms of the gradient in particle or molar density ρ i(particles or moles of i per cm 3) and a proportionality constant called the diffusion coefficient D iwith units of length square per unit of time. Fick proposed this simple flux law in 1855 for physical particles by analogy to Fourier’s law of heat conduction. With this representation of the flux, the one‐dimensional conservation equation of ρ i, often referred to as Fick’s second law, is

(1.2)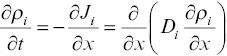

However, Fick’s law is known to be inadequate for representing the flux due to chemical diffusion in a multi‐component, non‐ideal system such as a silicate liquid. It cannot explain, for example, uphill diffusion, such as that shown later for Al 2O 3in Fig. 1.3, or that the rate of diffusion of a component in a multi‐component system depends on the direction of diffusion in composition space.

Onsager (1945) showed that a way to deal with transport in a multi‐component system is to express the diffusive flux of a component as a linear combination of the concentration gradients of all the independent components in the system. The one‐dimensional diffusive flux of component i in an n ‐component liquid is then given by

(1.3)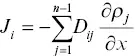

where D ijare elements of a ( n ‐1) by ( n ‐1) diffusion matrix with the n thcomponent taken as the dependent component. For example, equation 1.3for the ternary system CaO‐Al 2O 3‐SiO 2can be written in matrix form as

(1.4)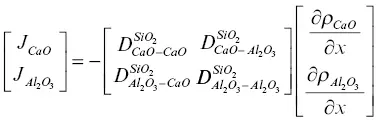

when SiO 2is taken as the dependent component. The flux of the SiO 2can be calculated using 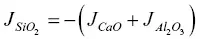or depending on the reference frame, by requiring that the sum of all the volume fluxes ν i J i( ν iis the molar volume of species i ) must add up to zero (see de Groot & Mazur, 1962).

Another issue that is especially relevant in natural silicate liquids is that the driving force for chemical diffusion is chemical potential gradients ∇ μ i( μ inow denotes chemical potential, not reduced mass). The more general version of equation 1.1is

(1.5)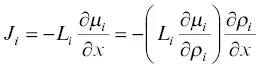

where the L iis called the phenomenological coefficient for diffusion and 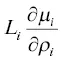is now identified as the diffusion coefficient for a non‐ideal binary system. The extension of this to a multi‐component system governed by a phenomenological diffusion matrix L i,jwas studied experimentally by Liang et al. (1966a; 1966b; 1967) with the non‐ideal molten CaO‐Al 2O 3‐SiO 2system.

When the formulation of the diffusive flux given previously is applied to multi‐component geologically relevant silicate materials, one is faced with the problem that to date only one complete diffusion matrix for an igneous melt (an 8‐component basaltic melt) has been reported (Guo & Zhang, 2018). When there is a lack of a full diffusion matrix for a specific system of interest, what is commonly done is to represent the multi‐component system as if it were a binary system made up of the component of interest with all the other components taken together as a second component. The mass flux in such a pseudo‐binary system will involve a single diffusion coefficient (i.e., n = 2 in equation 1.3) and thus given a diffusion profile of a component i one can in most cases fit the data using equation 1.2to determine the effective binary diffusion coefficient 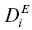for component i . Cooper (1968) showed how the effective binary diffusion coefficient of a given component is related to the full diffusion matrix of the system, and he also pointed out that effective binary diffusion coefficients depend not only on the local composition and thermodynamic state (e.g., temperature and pressure) but also on the direction of the diffusive flux in composition space. It follows from this that in order to determine the appropriate effective binary diffusion coefficient for modeling a natural diffusion profile, one needs to run an experiment with a diffusion couple juxtaposing compositions that are as close as possible to those of the far‐field values of the natural system.