The kinetic isotope fractionation factor α ijis the key parameter for calculating the isotopic evolution of vacuum evaporation residues as a function of the amount of the parent element evaporated when diffusion in the residue was sufficiently fast to continuously homogenize the residue. To arrive at this formulation as a form of Rayleigh fractionation consider the mass conservation equation of a uniformly distributed isotope i in a volume V bounded by a surface of area A , which is dN i/dt =− J i A , where N iis the total atoms of isotope i in V . A similar conservation equation applies for isotope j . Taking the ratio of the two conservation equations and using equation 1.11for the ratio of flux gives
(1.12) 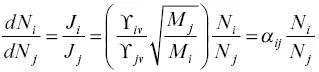
which when rearranged becomes
(1.13) 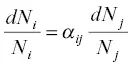
Integrating equation 1.13from an initial state with isotopic abundances N i, oand N j, oto a later state when the abundances have become N iand N jgives
(1.14) 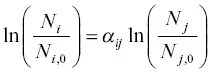
Applying the exponential function to both sides of this equation it becomes 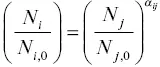 , which dividing by
, which dividing by 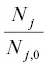 and rearranging gives
and rearranging gives 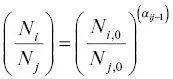 . Writing the isotope ratios as
. Writing the isotope ratios as 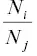 as R i, jand
as R i, jand 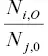 as R oone arrives at the Rayleigh fractionation equation for the evaporation residue
as R oone arrives at the Rayleigh fractionation equation for the evaporation residue
(1.15) 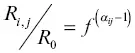
where 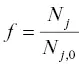 . This Rayleigh equation states that the isotopic ratio of a continuously homogenized condensed phase with initial ratio R obecomes R i, jwhen a fraction f of the initial amount of isotope j remains in the residue (or when a fraction 1– f had evaporated). In most practical application one can replace
. This Rayleigh equation states that the isotopic ratio of a continuously homogenized condensed phase with initial ratio R obecomes R i, jwhen a fraction f of the initial amount of isotope j remains in the residue (or when a fraction 1– f had evaporated). In most practical application one can replace 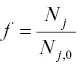 by the fraction of the parent element remaining in the residue. Equation 1.15shows that given an experimentally determined value of α ijand the degree of isotopic fractionation of an evaporation residue one can calculate how much of the parent element evaporated (i.e., 1– f ).
by the fraction of the parent element remaining in the residue. Equation 1.15shows that given an experimentally determined value of α ijand the degree of isotopic fractionation of an evaporation residue one can calculate how much of the parent element evaporated (i.e., 1– f ).
1.6.3. High‐Temperature Vacuum Evaporation Experiments
The experiments involving the evaporation of CAI‐like liquids described in this section were run at the University of Chicago in a high‐temperature vacuum furnace (pressure < 10 –6Torr) that was designed and constructed by Akihiko Hashimoto (see Hashimoto, 1990, for a description of the furnace). The experimental methods for evaporating molten samples in this furnace are described in the first paper documenting high‐temperature isotopic fractionations of evaporation residues from a silicate liquid (molten fayalite) by Davis et al. (1990). For CAI evaporation experiments powders of CAI‐like CMAS composition (CaO+MgO+SiO 2+Al 2O 3) were loaded onto small iridium wire loops (1–6 mm in diameter) that were then placed for different lengths of time in the hot spot of the vacuum furnace at temperatures between 1600°C and 1900°C and pressure less than 10 –6Torr. The objective of the evaporation experiments was to determine the evaporation coefficients γ Mgand γ Sifor calculating the fluxes using equation 1.10and the isotopic fractionation coefficients α Mgand α Sifor calculating the isotopic fractionation of evaporation residues using equation 1.15. When calculating the bulk composition of evaporation residues, one assumes CaO and Al 2O 3are effectively conserved, being much too refractory to significantly evaporate while there is still any MgO left in the melt.
The evaporation coefficients γ Mgand γ Siare determined by the amount of initial magnesium and silicon lost by evaporation from a molten bead of a given surface area as a function of temperature and run duration. The evaporation coefficients of magnesium and silicon are very similar to each other and decrease with temperature from about 0.2 at 1900°C to about 0.05 at 1500°C (see Fig. 3 in Richter et al., 2007). The kinetic isotope fractionation factors α Mgand α Siare determined by fitting the isotopic fractionation of evaporation residues as a function of the fraction of the initial amount of the parent element remaining in the residue with calculations using the Rayleigh fractionation equation ( equation 1.15). Fig. 1.17shows the isotopic fractionation of magnesium and silicon of evaporation residues of a CAI‐like melt from vacuum evaporation experiments run for different lengths of time by Richter et al. (2007) and Knight (2009). The curved profiles are fits to the data calculated assuming perfect Rayleigh fractionation ( equation 1.15) with α Mg= 0.9855 for 25Mg/ 24Mg and α Si= 0.0990 for 29Si/ 30Si. The fits are sufficiently good to confirm not only that the vacuum evaporation was a Rayleigh process but also that α Mgand are α Sido not significantly change as the composition of the evaporating material evolves by evaporation of its volatile components MgO and SiO 2. The experimentally determined value α Mg= 0.9855 is significantly larger (i.e., significantly less fractionation) than the inverse square root of the atomic mass of 24Mg/ 25Mg (0.9797). In the case of silicon, α Si= 0.9901 is only slightly larger than the inverse square root the mass ratio 29Si 16O/ 30Si 16O (0.9890). A more detailed analysis of the magnesium isotope fractionation data in Fig. 1.17showed that when the data from experiments run at different temperatures are fit separately with Rayleigh fractionation curves, the α Mgincreased (i.e., became less fractionating) as the temperature declined from 1900°C to 1600°C (see figure 10 in Richter et al., 2007). This temperature dependence of α Mgmust be extrapolated from the high temperature of the evaporation experiments down to temperatures in the range of 1450°C to 1300°C, at which the Type B CAIs were molten. If one were to use α Mgas given by the inverse square root law in the Rayleigh fractionation equation to invert the isotopic fractionation of a CAI for the amount of the parent element evaporated, it would result in an estimate of about a factor of two more magnesium evaporated compared to that calculated with α Mgderived by extrapolating the experimental values down to 1400°C. Using the experimentally determined α Mgand α Siis particularly important when using the magnesium isotopic fractionation of a CAI to determine the bulk composition of its pre‐evaporation precursor.
Читать дальше

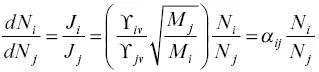
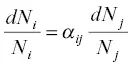
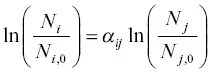
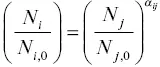 , which dividing by
, which dividing by 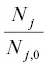 and rearranging gives
and rearranging gives 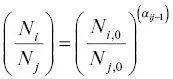 . Writing the isotope ratios as
. Writing the isotope ratios as 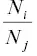 as R i, jand
as R i, jand 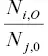 as R oone arrives at the Rayleigh fractionation equation for the evaporation residue
as R oone arrives at the Rayleigh fractionation equation for the evaporation residue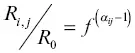
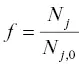 . This Rayleigh equation states that the isotopic ratio of a continuously homogenized condensed phase with initial ratio R obecomes R i, jwhen a fraction f of the initial amount of isotope j remains in the residue (or when a fraction 1– f had evaporated). In most practical application one can replace
. This Rayleigh equation states that the isotopic ratio of a continuously homogenized condensed phase with initial ratio R obecomes R i, jwhen a fraction f of the initial amount of isotope j remains in the residue (or when a fraction 1– f had evaporated). In most practical application one can replace 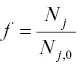 by the fraction of the parent element remaining in the residue. Equation 1.15shows that given an experimentally determined value of α ijand the degree of isotopic fractionation of an evaporation residue one can calculate how much of the parent element evaporated (i.e., 1– f ).
by the fraction of the parent element remaining in the residue. Equation 1.15shows that given an experimentally determined value of α ijand the degree of isotopic fractionation of an evaporation residue one can calculate how much of the parent element evaporated (i.e., 1– f ).










