Amir Sadr - Mathematical Techniques in Finance

In Chapter 6, we use the risk‐neutral framework to derive the Black‐Scholes‐Merton (BSM) option pricing formula by modeling asset returns as the continuous‐time limit of a random walk, that is a Brownian motion with risk‐adjusted drift. We recover and investigate the underlying replicating portfolio by considering the option Greeks: delta, gamma, theta. The interplay between these is shown by applying the Ito's lemma to the diffusion process driving an underlying asset and its derivative, leading to the BSM partial differential equation and its solution via methods from the classical boundary value heat equations.

We discuss the Cox‐Ross‐Rubinstein (CRR) model as a popular and practical computational method for pricing options that can also be used to compute the price of options with early exercise features via the backward induction algorithm from dynamic programming. For path‐dependent options such as barrier or averaging options, we present numerical models such as the Monte Carlo simulation models and variance reduction techniques.

Chapter 7introduces interest rate swaps and their derivatives used in structured finance. A plain vanilla swap can be priced via a static replication argument from a bootstrapped discount factor curve. In practice, simple European options on swaps and interest rate products are priced and risk‐managed via the normal version of Black's formula for futures. We introduce this model under the risk‐neutral pricing framework and show the pricing of the mainstream cap/floors, European swaptions, and CMS products. For complex derivatives, one needs a model for the evolution of multiple maturity zero‐coupon bonds in a risk‐neutral framework. We present the popular Hull‐White mean‐reverting model for the short rate and show the typical implementation methods and techniques, such as the forward induction method for yield curve inversion. We show the pricing of Bermudan swaptions via these lattice models. We conclude our discussion by presenting methods for calculating interest rate curve risk and VaR.

The end‐of‐chapter exercises are based on real‐world markets and products and delve deeper into some financial products and highlight the details of applying the techniques to them. All exercises can be solved by using a spreadsheet package like Excel. The Python projects are longer problems and can be done by small groups of students as a term project.

It is my hope that by the end of this book, readers have obtained a good toolkit of mathematical techniques, methods, and models used in financial markets and products, and their interest is piqued for a deeper journey into quantitative finance.

—Amir Sadr

New York, New York

December 2021

One learns by teaching and I have learned much from my students at NYU. Many thanks to all of my students over the years who have asked good questions and kept me on my toes.

Thanks to my editors at John Wiley & Sons: Bill Falloon, Purvi Patel, Samantha Enders, Julie Kerr, and Selvakumaran Rajendiran for patiently walking me through this project and correcting my many typos. All remaining errors are mine, and I welcome any corrections, suggestions, and comments sent to asadr@panalytix.com.

A.S.

Amir Sadrreceived his PhD from Cornell University with his thesis work on the Foundations of Probability Theory. After working at AT&T Bell Laboratories, he started his Wall Street career at Morgan Stanley, initially as a Vice President in quantitative modeling and development of exotic interest rate models, and later as an exotics trader. He founded Panalytix, Inc., to develop financial software for pricing and risk management of interest rate derivatives. He was a Managing Director for proprietary trading at Greenwich Capital, Senior Trader in charge of CAD exotics and USD inflation trading at HSBC, the COO of Brevan Howard U.S. Asset Management in the United States, and co‐founder of Yield Curve Trading, a fixed income proprietary trading firm. He is currently a partner at CorePoint Partners and is focused on crypto and DeFi.

bpbasis points, 1% of 1%, 0.0001 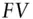future valueIRRinternal rate of returnPnLprofit and loss 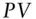present valueYTMyield to maturityp.a.per annum 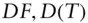discount factor, today's value unit payment at future date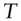 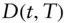dicount factor at 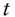for unit payment at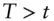 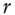interest rate 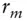compounding interest rate with 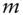compoundings per year 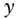yieldAPRannual percentage rate – stated interest rate without any compoundingsAPYannual pecentage yield – yield of a deposit taking compoundings into consideration: 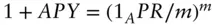for 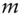compoundings per yearCFcash flow 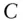coupon rate 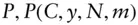price of an 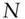‐year bond with coupon rate 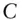, paid 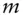times per year, with yield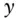 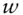accrual fraction between 2 dates according to some day count basis clean price of a bond = Price accrued interest 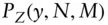price of an 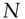‐year zero‐coupon bond with yield 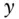, 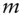compoundings per year 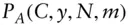price of an 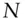‐year annuity with annuity rate of 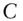, paid 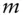times per year, with yield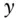 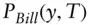price of 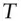‐maturity Treasury Bill with discount yield 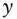PV01present value change due to an ”01” bp change in yieldPVBPpresent value change due to a 1 bp change in coupon, present value of a 1 bp annuity 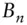balance of a level pay loan after 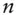periods 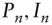principal and interest payments of a level pay loan in the 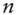th period 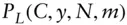price of 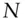‐year level pay loan with loan rate of 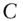, paid 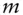times per year, with yield 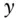ALaverage life 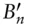balance of a level pay loan after 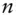periods with prepayments 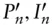principal and interest payments of a level pay loan within the 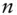th period with prepaymentsSMMsingle monthly mortality rateCPRconstant prepayment ratio 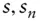periodic prepayment speed 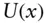utility of wealth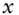 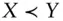lottery 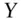is preferred to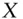 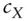certainty‐equivalent of random payoff 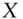, 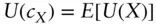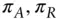absolute risk premium, relative risk premium 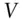, , 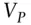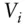value, value of a portfolio, value of 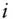th asset 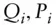quantity, price 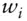weight of 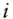th asset in a portfolio,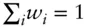 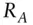return of an asset over a period : 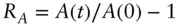. 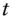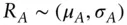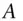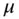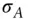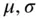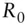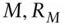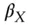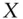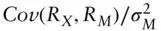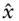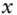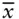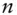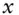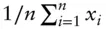Can be divided by to give rate of return asset 's return, with mean and standard deviation , Cmean vector, standard deviation vector, and covariance matrix of asset returns return of a risk‐free asset market portfolio, return of the market portfolio beta of an asset , empirical estimate of arithmetic average of samples of , 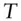forward date, future date 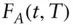forward value of asset 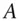at time 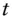for forward date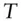 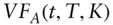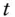‐value of a forward agreement on asset 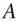for forward date 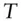and price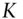 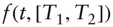simple (noncompounding) forward rate that can be locked at 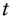for forward deposit period 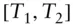. The first term may be omitted when 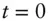. 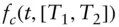continuously compounding forward rate that can be locked at 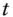for forward deposit period 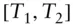. 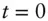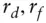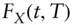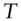The first term may be omitted when .FXforeign currency exchange rate domestic and foreign interest rates for forward exchange rate calculations the ‐forward exchange rate that can be locked at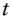 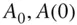today's value of an asset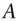 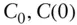today's value of a contingent claim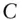 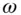generic random sample path 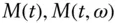value of a money‐market account at time 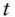along sample path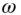 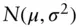normal or Gaussian random variable with mean 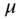and variance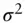 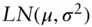lognormal random variable whose log is 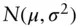CDFcumulative ditribution functionpdfprobability density functionpmfprobability mass function 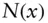cumulative distribution function of a standard ( 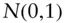) normal random variable,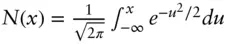 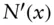probability density function of a standard normal random variable, 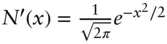BMBrownian motion 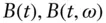Brownian motion at time 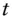along sample path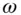 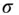proportional, lognormal volatilityATM, ATMFat‐the‐money spot, at‐the‐money forward 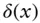Dirac's delta function,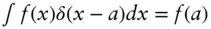 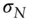absolute, normalized volatilityCMSconstant maturity swap rateAD, 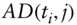Arrow‐Debreu price, today's price of unit payoff at state 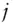on future date 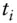i.i.d.independent and identically distributed