Figure 5.7Profile log‐likelihoods for self‐similar models of intrinsic order 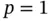 , as a function of the index
, as a function of the index 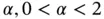 , both without a nugget effect (dashed line) and with a nugget effect (solid line). In addition, the log‐likelihood for each
, both without a nugget effect (dashed line) and with a nugget effect (solid line). In addition, the log‐likelihood for each 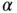 , with the parameters estimated by MINQUE (described In Section 5.13), is shown (dotted line).
, with the parameters estimated by MINQUE (described In Section 5.13), is shown (dotted line).
Figure 6.1Mercer–Hall data: bubble plot. See Example 6.1 for an interpretation.
Figure 6.2A plot of the sample and two fitted covariance functions (“biased‐mom‐ML”) for a CAR model fitted to the leftmost 13 columns of the Mercer–Hall data (Example 6.1). The data have been summarized by the biased sample covariance function. The four panels show the covariance function in the four principal directions with the sample covariances (open circles) together with the fitted covariances using moment estimation (solid lines) and maximum likelihood estimation (dashed lines).
Figure 6.3A plot of the sample and two fitted covariance functions (“fold‐mom‐ML”) for a CAR model fitted to the leftmost 13 columns of the Mercer–Hall data (Example 6.2). The data have been summarized by the folded sample covariance function. The four panels show the covariance function in the four principal directions with the sample covariances (open circles) together with the fitted covariances using moment estimation (solid lines) and maximum likelihood estimation (dashed lines).
Figure 6.4Relative efficiency of the composite likelihood estimator in AR(1) model relative to the ML estimator.
Figure 7.1Kriging predictor for 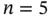 data points assumed to come from a stationary random field with a squared exponential covariance function 7.55, without a nugget effect, with mean 0. Panels (a)–(c) show the kriging predictor for three choices of the range parameter,
data points assumed to come from a stationary random field with a squared exponential covariance function 7.55, without a nugget effect, with mean 0. Panels (a)–(c) show the kriging predictor for three choices of the range parameter, 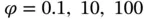 , respectively. Each panel shows the true unknown shifted sine function (solid), together with the fitted kriging curve (dashed), plus/minus twice the kriging standard errors (dotted).
, respectively. Each panel shows the true unknown shifted sine function (solid), together with the fitted kriging curve (dashed), plus/minus twice the kriging standard errors (dotted).
Figure 7.2Kriging predictor for 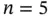 data points assumed to come from a stationary random field with a squared exponential covariance function 7.55, plus a nugget effect, with mean 0. The size of the relative nugget effect in Panels (a)–(c) is given by
data points assumed to come from a stationary random field with a squared exponential covariance function 7.55, plus a nugget effect, with mean 0. The size of the relative nugget effect in Panels (a)–(c) is given by 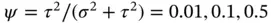 , respectively. Each panel shows the true unknown shifted sine function (solid), together with the fitted kriging curve (dashed), plus/minus twice the kriging standard errors (dotted).
, respectively. Each panel shows the true unknown shifted sine function (solid), together with the fitted kriging curve (dashed), plus/minus twice the kriging standard errors (dotted).
Figure 7.3Panel (a) shows the interpolated kriging surface for the elevation data, as a contour map. Panel (b) shows a contour map of the corresponding kriging standard errors. This figure is also included in Figure 1.3.
Figure 7.4Panel (a) shows a contour plot for the kriged surface fitted to the bauxite data assuming a constant mean and an exponential covariance function for the error terms. Panel (b) shows the same plot assuming a quadratic trend and independent errors. Panels (c) and (d) show the kriging standard errors for the models in (a) and (b), respectively.
Figure 7.5Kriging predictor and kriging standard errors for 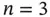 data points assumed to come from an intrinsic random field,
data points assumed to come from an intrinsic random field, 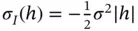 , no nugget effect. The intrinsic drift is constant. Panel (a): no extrinsic drift; Panel (b): linear extrinsic drift. Each panel shows the fitted kriging curve (solid), plus/minus twice the kriging standard errors (dashed).
, no nugget effect. The intrinsic drift is constant. Panel (a): no extrinsic drift; Panel (b): linear extrinsic drift. Each panel shows the fitted kriging curve (solid), plus/minus twice the kriging standard errors (dashed).
Figure 7.6Panel (a) shows the interpolated kriging surface for the gravimetric data, as a contour map. Panel (b) shows a contour map of the corresponding kriging standard errors.
Figure 7.7Kriging predictors for Example 7.6. For Panel (a), the kriging predictor is based on value constraints at sites 1,2,3. For Panel (b), the kriging predictor is additionally based on derivative constraints at the same sites.
Figure 7.8Deformation of a square (a) into a kite (b) using a thin‐plate spline. The effect of the deformation on 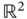 can also be visualized: it maps a grid of parallel lines to a bi‐orthogonal grid.
can also be visualized: it maps a grid of parallel lines to a bi‐orthogonal grid.
Figure B.1Creators of Kriging: Danie Krige and Georges Matheron.
Figure B.2Letter from Matheron to Mardia, dated 1990.
Figure B.3Translation of the letter from Matheron to Mardia, dated 1990.
Table 1.1Illustrative data 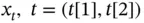 , on a
, on a 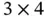 regular grid, represented in various ways,
regular grid, represented in various ways, 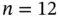 .
.
Table 1.2Elevation data: elevation 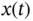 in feet above the sea level, where
in feet above the sea level, where 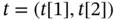 ,
, 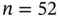 .
.
Table 1.3Bauxite data: percentage ore grade for bauxite at 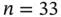 locations.
locations.
Table 1.4Gravimetric data: local gravity measurements in Quebec, Canada.
Table 1.5Semivariograms in each direction for the gravimetric data.
Table 1.6Soil data: surface pH in on an 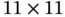 grid.
grid.
Table 1.7Mercer–Hall wheat yield (in lbs.) for 20 (rows) 25 (columns) agricultural plots (Mercer and Hall, 1911), where top–bottom corresponds to West–East, and left–right corresponds to North–South.
Table 1.8Aggregated Mercer–Hall wheat data for plots aggregated into blocks, giving the array layout for the blocks, the block dimensions, the block size 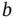 (number of plots in each block), the number of blocks
(number of plots in each block), the number of blocks 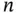 , and sample variance
, and sample variance 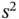 .
.
Читать дальше

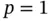 , as a function of the index
, as a function of the index 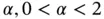 , both without a nugget effect (dashed line) and with a nugget effect (solid line). In addition, the log‐likelihood for each
, both without a nugget effect (dashed line) and with a nugget effect (solid line). In addition, the log‐likelihood for each 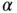 , with the parameters estimated by MINQUE (described In Section 5.13), is shown (dotted line).
, with the parameters estimated by MINQUE (described In Section 5.13), is shown (dotted line).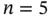 data points assumed to come from a stationary random field with a squared exponential covariance function 7.55, without a nugget effect, with mean 0. Panels (a)–(c) show the kriging predictor for three choices of the range parameter,
data points assumed to come from a stationary random field with a squared exponential covariance function 7.55, without a nugget effect, with mean 0. Panels (a)–(c) show the kriging predictor for three choices of the range parameter, 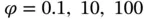 , respectively. Each panel shows the true unknown shifted sine function (solid), together with the fitted kriging curve (dashed), plus/minus twice the kriging standard errors (dotted).
, respectively. Each panel shows the true unknown shifted sine function (solid), together with the fitted kriging curve (dashed), plus/minus twice the kriging standard errors (dotted).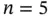 data points assumed to come from a stationary random field with a squared exponential covariance function 7.55, plus a nugget effect, with mean 0. The size of the relative nugget effect in Panels (a)–(c) is given by
data points assumed to come from a stationary random field with a squared exponential covariance function 7.55, plus a nugget effect, with mean 0. The size of the relative nugget effect in Panels (a)–(c) is given by 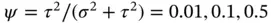 , respectively. Each panel shows the true unknown shifted sine function (solid), together with the fitted kriging curve (dashed), plus/minus twice the kriging standard errors (dotted).
, respectively. Each panel shows the true unknown shifted sine function (solid), together with the fitted kriging curve (dashed), plus/minus twice the kriging standard errors (dotted).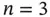 data points assumed to come from an intrinsic random field,
data points assumed to come from an intrinsic random field, 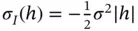 , no nugget effect. The intrinsic drift is constant. Panel (a): no extrinsic drift; Panel (b): linear extrinsic drift. Each panel shows the fitted kriging curve (solid), plus/minus twice the kriging standard errors (dashed).
, no nugget effect. The intrinsic drift is constant. Panel (a): no extrinsic drift; Panel (b): linear extrinsic drift. Each panel shows the fitted kriging curve (solid), plus/minus twice the kriging standard errors (dashed).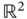 can also be visualized: it maps a grid of parallel lines to a bi‐orthogonal grid.
can also be visualized: it maps a grid of parallel lines to a bi‐orthogonal grid.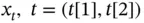 , on a
, on a 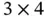 regular grid, represented in various ways,
regular grid, represented in various ways, 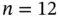 .
. in feet above the sea level, where
in feet above the sea level, where 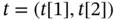 ,
, 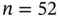 .
.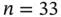 locations.
locations.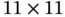 grid.
grid. (number of plots in each block), the number of blocks
(number of plots in each block), the number of blocks 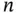 , and sample variance
, and sample variance 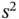 .
.










