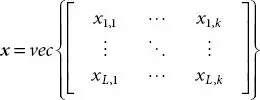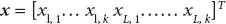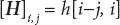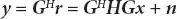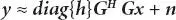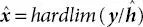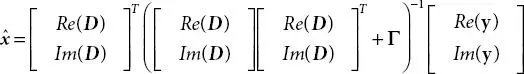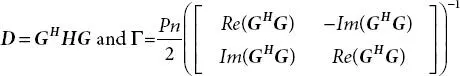(1.5) 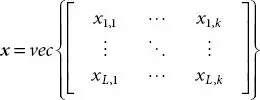
(1.6) 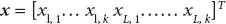
we can write the combined sampled transmit signal S∈ CN × 1 as
(1.7) 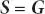
The impulse response under multipath fading in a time-variant channel can be expressed as matrix H∈ CN × N , whose entries are given by [2],
(1.8) 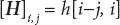
Finally, the received symbol is projected using received waveform to obtain
(1.9) 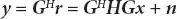
where nrepresents the additive noise term which is usually modeled as Gaussian random variable.
1.4 Existing Methods for Equalization in FBMC
1.4.1 One-Tap Zero Forcing Equalizer
In [7], a one-tap zero forcing equalizer for the FBMC system is considered. In this work, it is assumed that self-interference is ignored. Thus, the output of the FBMC system can be formulated as:
(1.10) 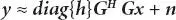
where his the vector obtain by vectorizing the channel matrix H. Thus, if ĥ represents the channel estimate, the output of the one-Tap equalizer will be obtained as:
(1.11) 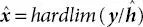
Where hardlimrepresents the hard limiter.
1.4.2 MMSE Block Equalizer
The conventional way to design an MMSE equalizer is to use complex-valued symbols. Unfortunately, this does not work with FBMC-OQAM as this equalizer does not eliminate the imaginary interference. A modified MMSE equalization is formulated to solve this issue by putting real and imaginary parts together using the approach outlined in [11, 13]. This method is termed as full block MMSE equalization whose solution is given by
(1.12) 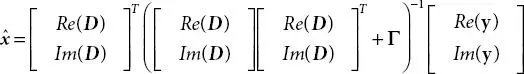
Where
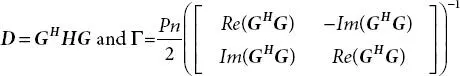
1.5 Proposed Machine Learning-Based FBMC Equalizer
In our proposed equalization scheme, we employ support vector machine (SVM) [16] to learn the required estimate using available input and output data. The SVM is a kind of kernel machine learning technique that utilizes a nonlinear mapping of the original training data [16]. It is mainly designed for binary classification, which was later extended to the multi-class problem. In supervised learning, when labeled training data is inputted, SVM outputs an optimal hyperplane, which categorizes new examples [17, 18]. The variants of SVM used in this study are Linear SVM, Quadratic SVM, and Cubic SVM [19, 20].
The main idea of the proposed equalizer is to learn the weight matrix for the FBMC equalizer via SVM using available training data { xtrain, ytrain}. Once the equalizer weight matrix is learned, the estimate for the unknown transmitted data xunknownis obtained by processing the received signal ytestthrough the designed SVM.
1.6 Results and Discussion
This section provides the results of the proposed machine learning-based equalizers for the FBMC system using LSVM, QSVM, and CSVM.
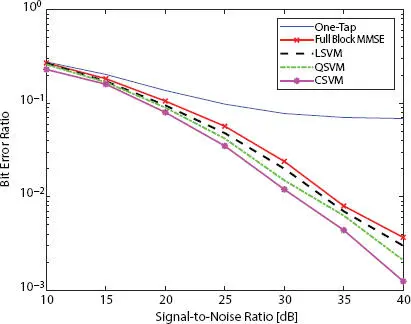
Figure 1.3BER performance comparison of different equalizers in FBMC system.
Table 1.1Performance comparison of SVM based FBMC equalizers.
| Performance measure |
LSVM |
QSVM |
CSVM |
| RMSE |
0.005951 |
0.005096 |
0.0048182 |
| Training Time (s) |
86.167 |
84.591 |
68.513 |
In this context, the FBMC system is simulated for 24 subcarriers and 30-time symbols. The prototype filter used is “Hermite” [13]. The results of BER are compared in Figure 1.3, which shows that the proposed SVM based equalizers have better performance than the full block MMSE equalizer of [13]. Moreover, it can be depicted from the results that the CSVM has the best performance among all the proposed methods.
In Table 1.1, the performances of the proposed SVM based equalizers are compared in terms of their testing RMSE and training time in seconds. Again, CSVM is found to be the best among other variants of SVM.
In this chapter, we study various methods of FBMC equalizers. We propose machine learning-based equalization techniques for the FBMC system. For this task, we develop the equalizer using three variants of SVM, namely Linear SVM, Quadratic SVM, and Cubic SVM. The BER performances of these methods are compared with that of the well-known One-Tap and Full Block MMSE equalizers. It was found from the simulation results that the proposed SVM based equalizer has better performance than that of the conventional methods. Moreover, the performances of the SVM based equalizers are compared among themselves in terms of RMSE and training time which shows that the CSVM outperformed the LSVM and QSVM in terms of both the RMSE and training time.
1. Farhang-Boroujeny, B., OFDM versus filter Bank multicarrier. IEEE Signal Process. Mag. , 28, 3, 92–112, May 2011.
2. Nissel, R., Schwarz, S., Rupp, M., Filter bank multicarrier modulation schemes for future mobile communications. IEEE J. Sel. Areas Commun. , 35, 1768–1782, 8, August 2017.
3. Nissel, R., Caban, S., Rupp, M., Experimental evaluation of FBMC-OQAM channel estimation based on multiple auxiliary symbols, in: IEEE Sensor Array and Multichannel Signal Processing Workshop (SAM) , Rio de Janeiro, Brazil, July 2016.
4. Nissel, R. and Rupp, M., Enabling low-complexity MIMO in FBMCOQAM, in: IEEE Globecom Workshops (GC Wkshps) , Dec 2016.
5. Nissel, R., Z¨ochmann, E., Lerch, M., Caban, S., Rupp, M., Low latency MISO FBMC-OQAM: It works for millimeter waves!, in: IEEE International Microwave Symposium , Honolulu, Hawaii, June 2017.
6. Nissel, R., Blumenstein, J., Rupp, M., Block frequency spreading: A method for low-complexity MIMO in FBMC-OQAM, in: IEEE International Workshop on Signal Processing Advances in Wireless Communications (SPAWC) , Sapporo, Japan, Jul 2017.
Читать дальше