enabling values of ETeff and νTeff to be determined.
4.7 Relationship between Two-phase and Multiphase Formulae
An interesting question is whether the formulae for the effective properties of multiphase composites can be derived from results that are valid only for two-phase composites. The results ( 4.10), ( 4.66)–( 4.69), ( 4.91), ( 4.147) and ( 4.152) are mixtures relations of the type
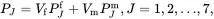 (4.153)
(4.153)
for the following combinations of properties:
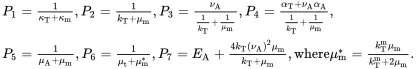 (4.154)
(4.154)
The properties PJ are effective properties of the unidirectional composite whereas PJf and PJm are the corresponding properties for the fibre and matrix, respectively. As Vf+Vm=1, relation ( 4.153) may now be written in the form
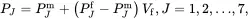 (4.155)
(4.155)
implying that the effective property PJ of a two-phase composite is the sum of the matrix value PJm and the product of the property difference PJf−PJm and the fibre volume fraction Vf. This approach can be extended to multiphase composites having N types of fibre reinforcement by generalising ( 4.155) to the following form:
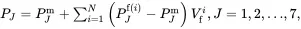 (4.156)
(4.156)
where PJf(i) is the value of the property PJ for the fibre of type i and Vfi is the corresponding fibre volume fraction. As, for the multiphase composite,
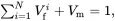 (4.157)
(4.157)
relation ( 4.156) may be expressed in the mixtures form
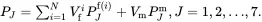 (4.158)
(4.158)
When the result ( 4.158) is applied to the properties defined in ( 4.154), relations ( 4.10), ( 4.66)–( 4.69), ( 4.91), ( 4.147) and ( 4.152) are generated. Thus, most multiphase properties can be derived from corresponding results for two-phase properties.
It should be noted that it has not been possible to derive the axial thermal expansion coefficient for a multiphase unidirectional composite, although the concentric cylinder model of a composite generates this property for a two-phase composite (see Appendix B). The challenge now is to determine the property combination P8 (≡αAeff) that enables the two-phase result (B.52) (see Appendix B) to be extended to multiphase composites using a relation of the form ( 4.158). Following inspection of the multiphase results so far obtained, one might expect that the required mixtures relation for a two-phase composite might have the following form:
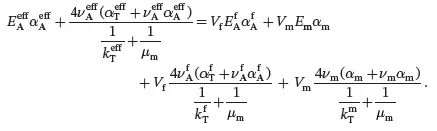 (4.159)
(4.159)
It can be shown that the conjectured relation ( 4.159) for just two phases is an equivalent form of the result (B.52) derived using the concentric cylinder model of a two-phase unidirectional composite. Relation ( 4.158) can then be used to generate the following corresponding expression which is conjectured to be valid for multiphase composites:
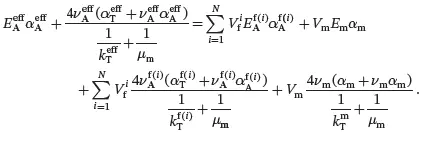 (4.160)
(4.160)
4.8 Summary of Results for Multiphase Composites
It is useful to bring together the results that have been derived for multiphase fibre-reinforced composites. The values of the effective properties κAeff, κTeff, EAeff, ETeff, νAeff, νteff, kTeff, μAeff, μteff, αAeff and αTeff of the transverse isotropic unidirectionally fibre-reinforced composite may be obtained from the following set of formulae, obtained from relations ( 4.10), ( 4.13), ( 4.66)–( 4.69), ( 4.91), ( 4.147), ( 4.152) and ( 4.160)
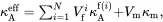 (4.161)
(4.161)
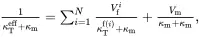 (4.162)
(4.162)
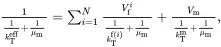 (4.163)
(4.163)
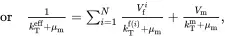 (4.164)
(4.164)
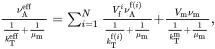 (4.165)
(4.165)
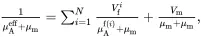 (4.166)
(4.166)
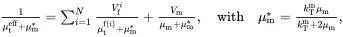 (4.167)
(4.167)
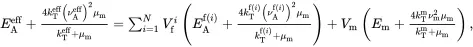 (4.168)
(4.168)
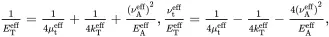 (4.169)
(4.169)
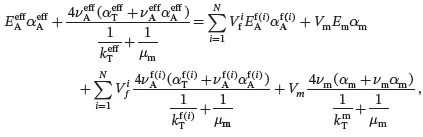 (4.170)
(4.170)
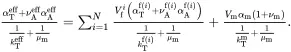 (4.171)
(4.171)
4.9 Results for Two-phase Fibre-reinforced Composites
For two-phase composites N = 1 so that, on writing Vf1=Vf=1−Vm, κAf(1)=κAf, κTf(1)=κTf, kTf(1)=kTf, μAf(1)=μAf, μtf(1)=μtf, EAf(1)=EAf, ETf(1)=ETf, νAf(1)=νAf, νtf(1)=νtf, αAf(1)=αAf and αTf(1)=αTf, the results of Section 4.8may be written as
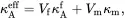 (4.172)
(4.172)
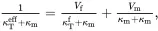 (4.173)
(4.173)
 (4.174)
(4.174)
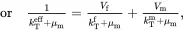 (4.175)
(4.175)
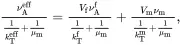 (4.176)
(4.176)
Читать дальше

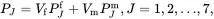 (4.153)
(4.153)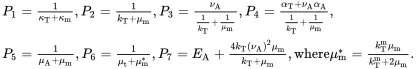 (4.154)
(4.154)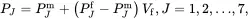 (4.155)
(4.155)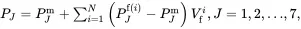 (4.156)
(4.156)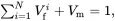 (4.157)
(4.157)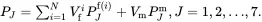 (4.158)
(4.158)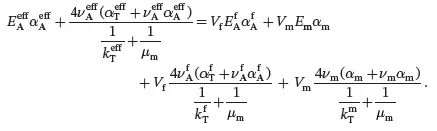 (4.159)
(4.159)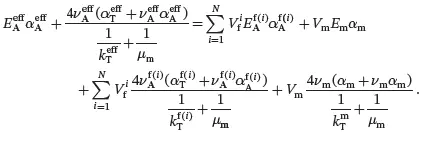 (4.160)
(4.160)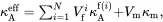 (4.161)
(4.161)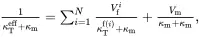 (4.162)
(4.162)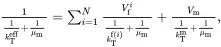 (4.163)
(4.163)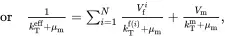 (4.164)
(4.164)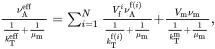 (4.165)
(4.165)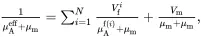 (4.166)
(4.166)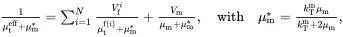 (4.167)
(4.167)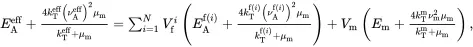 (4.168)
(4.168)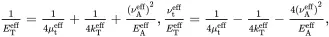 (4.169)
(4.169) (4.170)
(4.170)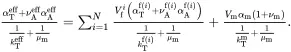 (4.171)
(4.171)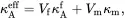 (4.172)
(4.172)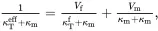 (4.173)
(4.173) (4.174)
(4.174)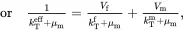 (4.175)
(4.175)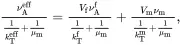 (4.176)
(4.176)










