and on subtraction that
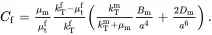 (4.132)
(4.132)
The substitution of ( 4.132) into ( 4.131) then leads to
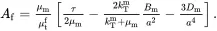 (4.133)
(4.133)
It now follows from ( 4.129) and ( 4.132) that
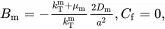 (4.134)
(4.134)
and from ( 4.130), ( 4.133) and ( 4.134) that
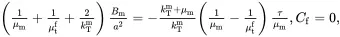 (4.135)
(4.135)
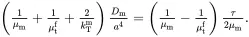 (4.136)
(4.136)
As Cf=0, it follows from ( 4.115)–( 4.117) that the stress and strain fields are uniform within the fibre. From ( 4.133) and ( 4.134)
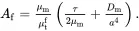 (4.137)
(4.137)
On substituting ( 4.136) into ( 4.137) to eliminate Dm , it can be shown that
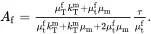 (4.138)
(4.138)
It should be noted that the displacement and stress fields in the fibre and the matrix can now be calculated. It is clear from ( 4.118)–( 4.121) that at large distances from the fibre the perturbations of the displacement and stress fields arising from the presence of the fibre are characterised by the values of the parameters Bm and Dm which are related according to relation ( 4.134) and depend on fibre properties. It is also clear that the far-field is insensitive to the actual location of the fibre. This means that a cluster of weakly interacting fibres can easily be considered, and this is the basis of Maxwell’s method, which is now described.
4.5.5 Applying Maxwell’s Approach to Multiphase Fibre Composites
Owing to the use of the far-field in Maxwell’s method for estimating the properties of fibre composites, it is possible to consider multiple fibre reinforcements. Suppose in a cluster of fibres that there are N different types such that for i = 1, …, N , there are nifibres of radius ai. The properties of the fibres of type i are denoted by a superscript i . The cluster is assumed to be homogeneous regarding the distribution of fibres, and leads to transverse isotropic effective properties.
Consider the following asymptotic form of radial displacement field in the matrix as r→∞ that is derived from ( 4.118)
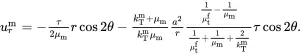 (4.139)
(4.139)
For the case of multiple phases, relation ( 4.139) is generalised to the following form
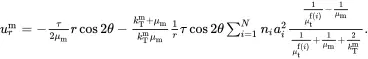 (4.140)
(4.140)
When the result ( 4.140) is applied to a single fibre of radius b having effective properties corresponding to the multiphase cluster of fibres, it follows that
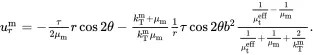 (4.141)
(4.141)
The cluster of all types of fibre is now considered to be enclosed in a cylinder of radius b such that the volume fraction of fibres of type i within the cylinder of radius b is given by Vfi=niai2/b2. The volume fractions must satisfy the relation
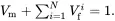 (4.142)
(4.142)
It then follows that ( 4.140) may be written in the form
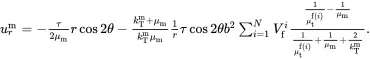 (4.143)
(4.143)
The coefficients of the 1/ r terms in relations ( 4.141) and ( 4.143) must be identical so that
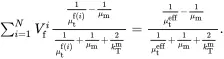 (4.144)
(4.144)
It then follows that the effective transverse shear modulus for the multiphase composite is given by
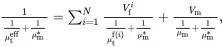 (4.145)
(4.145)
where
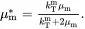 (4.146)
(4.146)
On using ( 4.1), the result ( 4.145) may also be written in the form
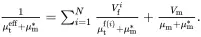 (4.147)
(4.147)
4.6 Other Effective Elastic Properties for Multiphase Fibre-reinforced Composites
Four independent effective elastic properties can now be estimated using relations ( 4.69), ( 4.67), ( 4.91) and ( 4.147), namely, νAeff,kTeff,μAeff,μteff. It is clear that Maxwell’s methodology has not provided an expression for the axial modulus EAeff of a multiphase unidirectionally fibre-reinforced composite. This problem has, however, been overcome [6] by considering a special case of aligned spheroidal inclusions (see Chapter 15for details and (15.100)) where it has been shown that the effective axial Young’s modulus EAeff may be obtained from the following formula
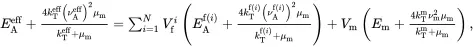 (4.148)
(4.148)
where
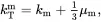 (4.149)
(4.149)
and where values of νAeff and kTeff have already been determined. The transverse Young’s modulus ETeff and transverse Poisson’s ratio νteff can be estimated by making use of the following relations, corresponding to ( 4.18) and ( 4.47),
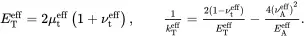 (4.150)
(4.150)
It follows that
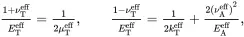 (4.151)
(4.151)
so that
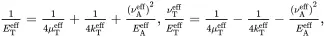 (4.152)
(4.152)
Читать дальше

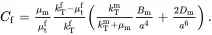 (4.132)
(4.132)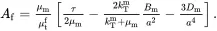 (4.133)
(4.133)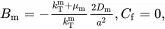 (4.134)
(4.134)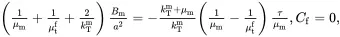 (4.135)
(4.135)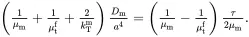 (4.136)
(4.136)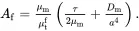 (4.137)
(4.137)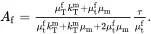 (4.138)
(4.138)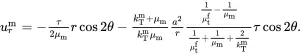 (4.139)
(4.139)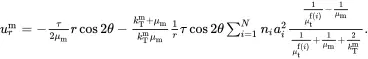 (4.140)
(4.140)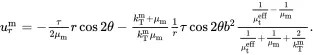 (4.141)
(4.141)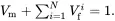 (4.142)
(4.142) (4.143)
(4.143) (4.144)
(4.144) (4.145)
(4.145) (4.146)
(4.146) (4.147)
(4.147)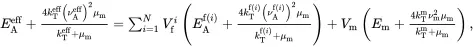 (4.148)
(4.148)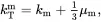 (4.149)
(4.149)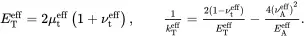 (4.150)
(4.150)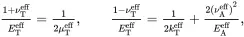 (4.151)
(4.151)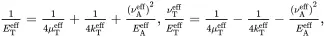 (4.152)
(4.152)










