Марио Ливио - Был ли Бог математиком? Галопом по божественной Вселенной с калькулятором, штангенциркулем и таблицами Брадиса

То есть исторический опыт показывает, что методом многочисленных проб и ошибок пифагорейцы и их последователи открыли способы строить определенные геометрические фигуры, которые для них воплощали важные понятия вроде любви и космоса. Тогда неудивительно, что и они, и Евклид, задокументировавший эту традицию, изобрели понятие золотого сечения, необходимого для этих построений, и дали ему название. В отличие от любого другого произвольного соотношения, число 1,618… стало предметом пристального изучения с богатой и интересной историей и даже в наши дни то и дело заявляет о себе в самых неожиданных местах. Например, спустя две тысячи лет после Евклида немецкий астроном Иоганн Кеплер открыл , что это число – чудесным образом – имеет отношение к последовательности чисел под названием числа Фибоначчи . Последовательность Фибоначчи – 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233,… – характерна тем, что каждый ее член, начиная с третьего, представляет собой сумму двух предыдущих (2 = 1 + 1; 3 = 1 + 2; 5 = 2 + 3 и так далее). А если поделить любой член последовательности на непосредственно предшествующий (например, 144 ÷ 89; 233 ÷ 144 и так далее), окажется, что отношения колеблются в окрестности золотого сечения, причем чем больше члены последовательности, тем ближе их отношения к золотому сечению. Например, при округлении до шестого знака после запятой у нас получатся следующие числа: 144 ÷ 89 = 1,617978; 233 ÷ 144 = 1,618056; 377 ÷ 233 = 1,618026 и так далее.

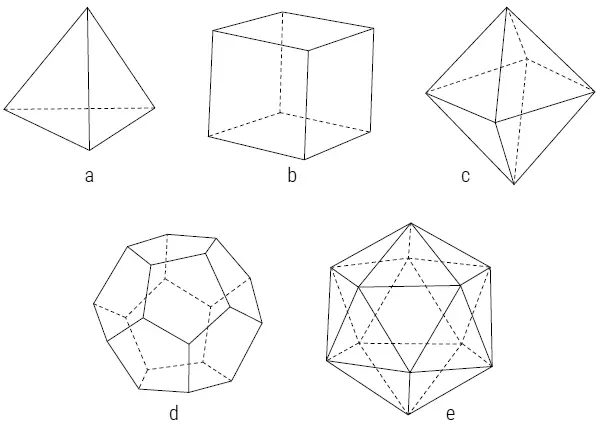
Рис. 65

В новое время выяснилось, что числа Фибоначчи и, соответственно, золотое сечение описывают расположение листьев на стеблях некоторых растений – это явление называется филлотаксис – и структуру кристаллов некоторых алюминиевых сплавов.

Почему я считаю определение золотого сечения, которое дал Евклид, изобретением? Потому что изобретательство Евклида выделило это соотношение из общей массы и привлекло к нему внимание математиков. С другой стороны, в Китае, где понятие золотого сечения не было изобретено, в математической литературе нет никаких упоминаний ни о чем похожем. В Индии, где его опять же не изобрели, оно вскользь затронуто лишь в нескольких второстепенных тригонометрических теоремах.

Примеров, которые показывают, что вопрос «Что есть математика – изобретение или открытие?» некорректно сформулирован, можно найти множество. Наша математика – это сочетание изобретений и открытий . Аксиомы евклидовой геометрии как понятия были изобретением, как и, скажем, правила игры в шахматы. Кроме того, аксиомы были дополнены различными изобретенными понятиями – треугольниками, параллелограммами, эллипсами, золотым сечением и тому подобным. А теоремы евклидовой геометрии, напротив, по большей части представляют собой открытия: это пути, связывающие разные понятия. В некоторых случаях доказательства приводили к формулировке новых теорем – математики изучали, что можно доказать, и из этого выводили теоремы. В других, как описано в «Методе» Архимеда, они сначала находили ответ на заинтересовавший их вопрос, а потом уже работали над доказательством.

Понятия – это, как правило, изобретения. Простые числа как понятие были изобретены, однако все теоремы о простых числах – открытия [158] Интересные идеи по этому поводу изложены в статье Иегуды Рава в Hersh 2000. . Математики древнего Вавилона, Египта и Китая не изобрели понятие простых чисел, хотя их математика достигла огромных успехов. Можно ли сказать, что они просто не «открыли» простые числа? Не в большей степени, чем заявить, что в Великобритании не «открыли» единую кодифицированную конституцию. Государство способно выжить и без конституции – и математика способна развиваться без понятия простых чисел. Так и получилось!

А известно ли нам, почему греки изобрели понятия вроде аксиом и простых чисел? Конечно, наверняка сказать нельзя, но можно предположить, что это произошло в ходе неустанных попыток исследовать самые фундаментальные составляющие Вселенной. Простые числа – это строительный материал чисел, точно так же как атомы – это строительный материал вещества. Подобным же образом аксиомы были источником, из которого должны вытекать все геометрические истины. Додекаэдр символизировал Вселенную в целом, а золотое сечение послужило понятием, благодаря которому этот символ был воплощен.