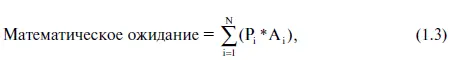Ральф Винс - Математика управления капиталом - Методы анализа риска для трейдеров и портфельных менеджеров

Короче говоря, ищите зависимость. Если она обнаружится с достаточно высокой вероятностью, тогда измените правила системы, чтобы использовать эту зависимость. В противном случае, при отсутствии убедительного статистического доказательства зависимости, считайте, что ее не существует (и вы понесете меньшие потери, если фактически зависимость все же существует).

Таким образом, вам лучше не торговать, пока не будет убедительных доказательств того, что рыночная система, по которой вы собираетесь торговать, прибыльна, т. е. пока вы не будете уверены, что рыночная система имеет положительное математическое ожидание.

Математическое ожидание является суммой, которую вы можете заработать или проиграть в среднем по каждой ставке. На языке азартных игроков это иногда называется «преимуществом игрока» (если оно положительно для игрока) или «преимуществом казино» (если оно отрицательно для игрока):

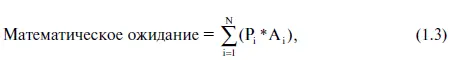
где Р – вероятность выигрыша или проигрыша;

A – выигранная или проигранная сумма;

N – количество возможных результатов.

Математическое ожидание – это сумма произведений каждого возможного выигрыша или проигрыша и вероятности такого выигрыша или проигрыша.

Давайте рассмотрим математическое ожидание игры, где у вас есть 50 % шансов выиграть 2 долл. и 50 % шансов проиграть 1 долл.:

Математическое ожидание = (0,5 * 2) + (0,5 * (–1)) = 1 + (–0,5) = 0,5.

В таком случае ваше математическое ожидание – выигрыш 50 центов в среднем за бросок.

Рассмотрим ставку на один номер в рулетке. В этом случае ваше математическое ожидание (МО) составит:

МО = ((1 / 38) * 35) + ((37 / 38) * (–1)) = (0,02631578947 * 35) + (0,9736842105 * (–1)) = (0,9210526315) + (–0,9736842105) = –0,05263157903.

Если вы поставите 1 долл. на номер в рулетке (американский двойной ноль), то можете ожидать проигрыш в среднем 5,26 цента на один круг. Если вы поставите 5 долл., то можете ожидать проигрыш в среднем 26,3 цента на один круг. Отметьте, что различные ставки имеют различное математическое ожидание в денежном выражении, но в процентном отношении от ставки оно всегда одинаково. Ожидание серии ставок является суммой значений ожиданий отдельных ставок . Поэтому если при игре в рулетку вы ставите 1 долл. на число, затем 10 долл. на число, затем 5 долл. на число, то вашим общим ожиданием будет:

МО = (–0,0526 * 1) + (–0,0526 * 10) + (–0,0526 * 5) = –0,0526 – 0,526 – 0,263 = –0,8416.

Таким образом, следует ожидать проигрыш 84,16 цента.

Этот принцип объясняет, почему системы, в которых пытаются изменить размер ставок в зависимости от того, сколько проигрышей или выигрышей было (допуская процесс независимых испытаний), считаются проигрышными. Сумма отрицательных ожиданий по ставкам всегда является отрицательным ожиданием!

В отношении управления капиталом очень важно понимать, что при игре с отрицательным ожиданием нет схемы управления деньгами, которая может сделать вас победителем. Если вы продолжаете играть, то независимо от способа управления деньгами вы проиграете весь ваш счет, каким бы большим он ни был в начале.

Эта аксиома верна не только для игры с отрицательным ожиданием, она истинна также для игры с равными шансами. Поэтому единственный случай, когда у вас есть шанс выиграть в долгосрочной перспективе, – это игра с положительным математическим ожиданием. Кроме того, вы можете выиграть только в двух случаях. Во-первых, при использовании ставки одинакового размера, во-вторых, используя ставки при f, меньшем значения f, соответствующего точке, в которой среднее геометрическое HPR становится равным или меньшим 1.

Эта аксиома истинна только при отсутствии верхнего поглощающего барьера. Например, азартный игрок, который начинает со 100 долл., прекращает играть, если его счет вырастает до 101 долл. Эта верхняя цель (101 долл.) называется поглощающим барьером. Допустим, игрок всегда ставит 1 долл. на красный цвет рулетки. Таким образом, у него небольшое отрицательное математическое ожидание. У игрока больше шансов увидеть, как его счет вырастет до 101 долл., и он должен будет прекратить играть, чем увидеть, как его счет уменьшится до нуля и он будет вынужден прекратить играть. Если он будет повторять этот процесс снова и снова, то окажется в отрицательном математическом ожидании. Если сыграть в такую игру только раз, то аксиома неизбежного банкротства, конечно же, неприменима. Различие между отрицательным и положительным ожиданием – это различие между жизнью и смертью. Не имеет значения, насколько положительное или насколько отрицательное ожидание; важно лишь то, положительное оно или отрицательное. Поэтому до рассмотрения вопросов управления капиталом вы должны найти игру с положительным ожиданием.