Ральф Винс - Математика управления капиталом - Методы анализа риска для трейдеров и портфельных менеджеров

Посмотрите на рис. 1.2. На нем изображены две абсолютно коррелированные последовательности. Мы называем это положительной корреляцией .

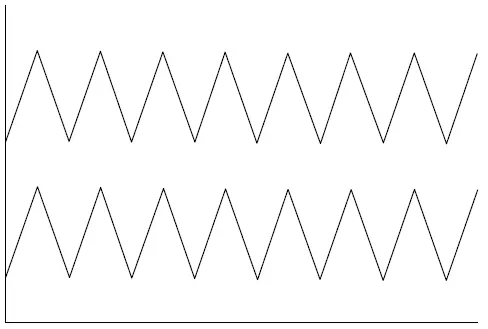
Рис. 1.2. Положительная корреляция (r = +1,00)

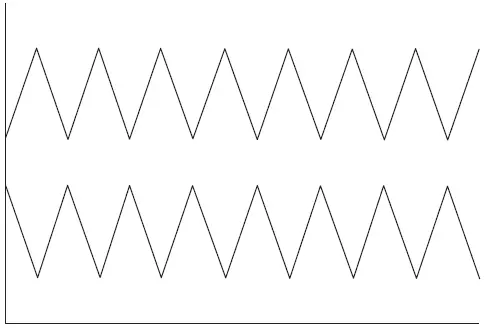
Рис. 1.3. Отрицательная корреляция (r = –1,00)

Теперь посмотрите на рис. 1.3. Он показывает две последовательности, которые находятся точно в противофазе. Когда одна линия идет вверх, другая следует вниз (и наоборот). Мы называем это отрицательной корреляцией .

Формула для коэффициента линейной корреляции r двух последовательностей Х и Y такова (черта над переменной обозначает среднее арифметическое значение):

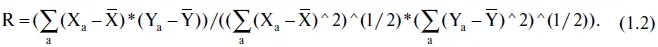
Расчет следует производить следующим образом.

1. Вычислите среднее Х и Y (т. е. 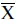и ).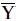

2. Для каждого периода найдите разность между Х и 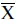, а также Y и .

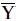3. Теперь рассчитайте числитель. С этой целью для каждого периода перемножьте ответы из шага 2, другими словами, для каждого периода умножьте разность между Х и 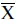на разность между Y и .

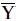4. Сложите результаты, полученные в шаге 3, за все периоды. Это и есть числитель.

5. Теперь найдите знаменатель. Для этого возьмите результаты шага 2 для каждого периода как для разностей Х, так и для разностей Y и возведите их в квадрат (теперь они будут положительными значениями).

6. Сложите возведенные в квадрат разности Х за все периоды. Проделайте ту же операцию с возведенными в квадрат разностями Y.

7. Извлеките квадратный корень из суммы возведенных в квадрат разностей Х, которые найдены в шаге 6. Теперь проделайте то же с Y, взяв квадратный корень суммы возведенных в квадрат разностей Y.

8. Умножьте два результата, которые вы нашли в шаге 7, т. е. умножьте квадратный корень суммы возведенных в квадрат разностей Х на квадратный корень суммы возведенных в квадрат разностей Y. Это и есть знаменатель.

9. Разделите числитель, который вы нашли в шаге 4, на знаменатель, который вы нашли в шаге 8. Это и будет коэффициент линейной корреляции r.

Значение r всегда будет между +1,00 и –1,00. Значение 0 указывает, что корреляции нет.

Теперь посмотрите на рис. 1.4. Он представляет следующую последовательность из 21 сделки:

1, 2, 1, –1, 3, 2, –1, –2, –3, 1, –2, 3, 1, 1, 2, 3, 3, –1, 2, –1, 3.

Чтобы понять, есть ли какая-либо зависимость между предыдущей и текущей сделкой, мы можем использовать коэффициент линейной корреляции. Для значений Х в формуле для r возьмем P&L по каждой сделке. Для значений Y в формуле для r возьмем ту же самую последовательность P&L, только смещенную на одну сделку. Другими словами, значение Y – это предыдущее значение Х (рис. 1.5).

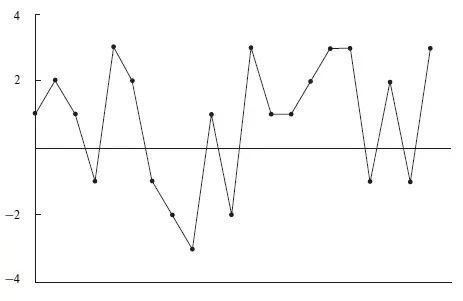
Рис. 1.4. Отдельные результаты 21 сделки

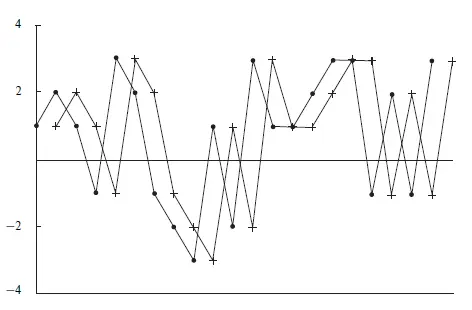
Рис. 1.5. Отдельные результаты 21 сделки, сдвинутые на 1 сделку

Средние значения различаются, потому что вы усредняете только те X и Y, которые частично перекрывают друг друга, поэтому последнее значение Y (3) не вносит вклад в 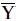, а первое значение Х (1) не вносит вклад в .

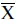Числитель является суммой всех значений из столбца Е (0,8). Чтобы найти знаменатель, мы извлечем квадратный корень из итогового значения столбца F и получим 8,555699, потом извлечем квадратный корень из итогового значения столбца G и получим 8,258329, затем перемножим их, что даст в результате 70,65578. Теперь разделим числитель 0,8 на знаменатель 70,65578 и получим 0,011322. Это наш коэффициент линейной корреляции r. В данном случае коэффициент линейной корреляции 0,011322 едва ли о чем-то говорит, но для многих торговых систем он может достигать бóльших значений. Высокая положительная корреляция (по крайней мере 0,25) говорит о том, что большие выигрыши редко сменяются большими проигрышами, и наоборот. Отрицательные значения коэффициента корреляции (между –0,25 и –0,30) подразумевают, что после больших проигрышей следуют большие выигрыши, и наоборот. Для заданного количества сделок с помощью метода, известного как преобразование Z Фишера, коэффициент корреляции можно преобразовать в доверительный уровень. Эта тема рассматривается в приложении C. Отрицательную корреляцию так же, как и положительную, можно использовать в своих интересах. Например, если обнаружена отрицательная корреляция и система показала большой проигрыш, то в следующей сделке можно ожидать большого выигрыша и, таким образом, открыть больше контрактов, чем обычно. 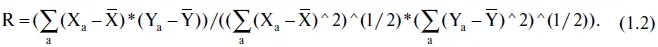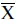Если и эта сделка принесет убыток, то он не должен быть очень большим (из-за отрицательной корреляции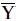).