Итак, в треугольнике с длинами сторон 3, 4 и 5 имеем
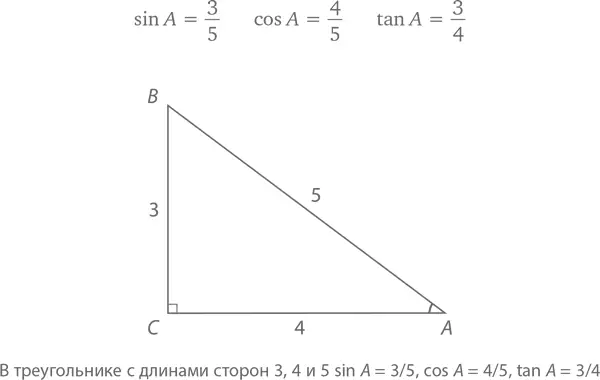
А что с углом B ? Аккуратно подсчитаем и получим

то есть синус B будет равен косинусу A , а косинус B – синусу A ! Волшебного в этом абсолютно ничего нет: просто сторона, противолежащая ∠ A , является прилежащей к ∠ B , и наоборот – сторона, прилежащая к ∠ A , является противолежащей ∠ B . Гипотенуза же у этих двух углов так и вовсе одна на двоих.
Так как ∠ A + ∠ B = 90°, мы можем сделать вывод, что для любого острого угла справедливо следующее:
sin (90° – A ) = cos A cos (90° – A ) = sin A
То есть если в треугольнике ABC ∠ A равен 40°, то при ∠ B = 50° sin 50° = cos 40°, а cos 50° = sin 40°. Другими словами, косинус данного угла (40°) равен синусу дополнительного (50°).
Кроме синуса, косинуса и тангенса в тригонометрии есть еще три элементарные функции. Используются они, правда, не так часто, как уже известные нам, но почему бы не упомянуть и их? Это секанс, косеканси котангенс, и смысл их заключается в том, что
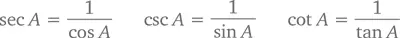
Приставка «ко-» означает здесь те же отношения дополнения, что и в паре «синус – косинус», а именно: для любого острого угла прямоугольного треугольника sec (90° – A ) = csc A , а tan (90° – A ) = cot A .
Чтобы найти косинусы, тангенсы и все остальное, достаточно знать значение синуса одного из углов, это очевидно. Но ведь и его (скажем, sin 40°) тоже надо как-то найти, правда? Самый простой способ – воспользоваться калькулятором: просто включаем его и узнаем, что sin 40° = 0,642…. Откуда это значение берется, мы узнаем чуть позже.
Некоторые значения тригонометрических функций встречаются в расчетах настолько часто, что лучше всего их просто запомнить. Вернемся к треугольнику с углами 30°, 60° и 90° и вспомним про соотношение его сторон – 1: √ 3 : 2. Получается, что
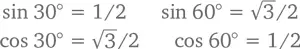
Стороны же треугольника с углами 45°, 45° и 90° имеют соотношение 1: 1: √ 2 , следовательно
sin 45° = cos 45° = 1/√ 2 = √ 2/2
А так как tan 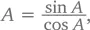 запомнить придется только то, что tan 45° = 1 и что tan 90° определить невозможно, потому что cos 90° = 0.
запомнить придется только то, что tan 45° = 1 и что tan 90° определить невозможно, потому что cos 90° = 0.
С такими знаниями пора вернуться к подножию нашей горы. Только сначала давайте остановимся у первого попавшегося дерева и попробуем рассчитать его высоту.
Предположим, что мы не дошли до ствола 3 метра и что угол между землей под нашими ногами и верхушкой дерева составляет 50°, как изображено на рисунке. (Определить угол, кстати, можно либо с помощью приложения, которое в наши дни есть на многих смартфонах, либо посредством простого устройства, называющегося клинометр , которое легко собирается из транспортира, соломинки для питья и канцелярской скрепки.)
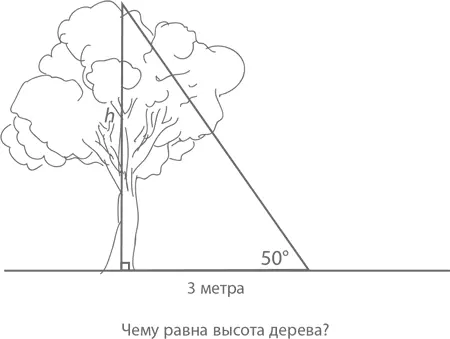
Обозначим высоту буквой h . То есть

Следовательно, h = 3 tan 50°. Последний, если верить калькулятору, равен 1,19…. Получаем 3(1,19…) ≈ 3,57, что и является высотой дерева.
Теперь пойдем к горе – испытаем первый из наших математических методов. Сложность его в том, что мы даже примерно не сможем прикинуть расстояние до центра подножья – то есть вместе с высотой горы мы получаем уравнение с двумя неизвестными. Предположим, что мы измерили угол от точки, в которой находимся, до вершины и получили 40°, потом отошли на 300 метров дальше и получили уже 32° (см. рисунок). Что нам теперь с этой информацией делать?
Способ 4 (метод тангенсов): Обозначим высоту горы h , а расстояние до центра ее подножья в изначальной позиции – буквой x (то есть x это длина отрезка CD ). Калькулятор говорит, что в треугольнике BCD tan 40° ≈ 0,839, следовательно
Читать дальше
Конец ознакомительного отрывка
Купить книгу



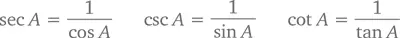
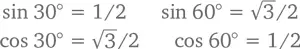
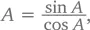 запомнить придется только то, что tan 45° = 1 и что tan 90° определить невозможно, потому что cos 90° = 0.
запомнить придется только то, что tan 45° = 1 и что tan 90° определить невозможно, потому что cos 90° = 0.











